Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 130

Para a viga uniforme mostrada, determinar a reação em B .  

Passo 1

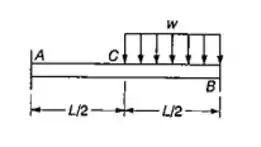
Fala aí galera, bora pra mais uma questão de Resmat. Neste exercício temos uma viga bi-engastada com carga uniformemente distribuída em metada da sua extensão. Primeiro, dividimos em 3 cass de superposição. São eles:

y 1 = P L 3 6 E I y 1 = R B L 3 6 E I  

Para o segundo carregamento, temos:

y 2 = - w 24 E I x 4 - 4 L x 3 + 6 L 2 x 2 y 2 = - w 24 E I L 4 - 4 L L 3 + 6 L 2 L 2 y 2 = - w L 4 8 E I

E para o terceiro, temos:

y 3 = - M 2 E I x 2 y 3 = - M B L 2 2 2 E I y 3 = - M B L 2 8 E I

Com isso, temos que a superposição em B é dada por:

y B = y 1 + y 2 + y 3 = 0 R B L 3 6 E I - w L 4 8 E I - M B L 2 8 E I = 0

Passo 2

Em seguida, para encontrarmos os momentos é necessária uma equação de compatibilidade. Logo, a partir do apêndice D do nosso livro, encontramos as seguintes relações de rotação nos apoios:

θ B = R B L 2 2 E I - w L 3 6 E I - M B L E I = 0

Nota-se que ficamos com um sistema linear. Resovlendo este sistema, vamos encontrar as reações de B . São elas:

R B = w L 4 E I M B = 4 w L 5 - w L 2 12 E I

Resposta

R B = w L 4 E I M B = 4 w L 5 - w L 2 12 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Antes do carregamento uniformemente distribuído ser aplicado, uma abertura δ 0 existe entre a viga de perfil laminado de aço W 410 × 60 e apoio C. Sabendo-se que E = 200 G P a , determinar o tamanho d
Antes da carga P ser aplicada, uma abertura δ 0 = 6,35m m existe entre a viga de perfil laminado de aço S 75 × 8,5 e o apoio B. Sabendo-se que E = 200 G P a e P = 11120N , determinar:A Reação em B.
Antes da carga P ser aplicada, uma abertura δ 0 = 6,35m m existe entre a viga de perfil laminado de aço S 75 × 8,5 e o apoio B. Sabendo-se que E = 200 G P a e P = 11120N , determinar:A deflexão em A.
Antes da carga P ser aplicada, uma abertura δ 0 = 6,35m m existe entre a viga de perfil laminado de aço S 75 × 8,5 e o apoio B. Sabendo-se que E = 200G P a , determinar a intensidade de P para que a d
Para a viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão em B . Usar E = 200G P a