Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 14
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no meio do vão: (a) a maior tensão normal; (b) a maior tensão de cisalhamento, usando a aproximação sugerida na Sec. 5.6.
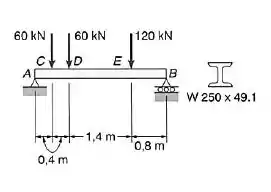
Passo 1
Para calcular o que ele pede nas alternativas, vamos precisar do momento de inércia da seção e dos esforços nela.
O momento de inércia, e outros dados dessa seção, a gente pega numa tabelinha de vigas de aba larga:
Já para os esforços, precisamos achar as forças de reação nos apoios e calcular o valor do momento e do cortante na seção que fica no meio da viga (a que o enunciado pede):
Olhando para a parte da viga que está à direita da seção e analisando os esforços:
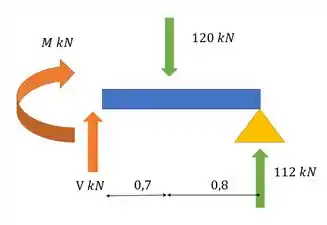
Temos
Passo 2
(a) Queremos a maior tensão normal na seção. Essa tensão vai ser causada pelo momento na seção, que vale:
E vai estar localizada no ponto na seção mais distante do eixo (linha neutra), que vale:
Agora é só a gente usar a fórmulinha de tensão normal devido a flexão:
Passo 3
(b) Para achar a tensão de cisalhamento vamos usar a aproximação sugerida:
A gente sabe que:
Podemos aproximar a área da alma multiplicando a espessura dela pela altura da viga:
Substituindo na fórmulinha:
Resposta
(a)
(b)