Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 93

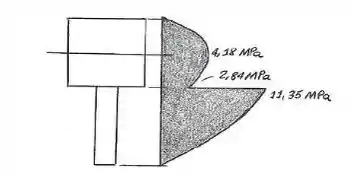
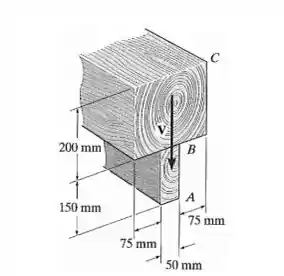
Faça um rascunho da intensidade da distribuição da tensão de cisalhamento que age na área da seção transversal da viga e determine a força de cisalhamento resultante que age no segmento AB. O cisalhamento que age na seção é V = 175 kN. Mostre que I N A = 340,82( 10 6 ) .

Passo 1

Fala aí galera, bora pra mais um problema de resmat. Neste problema, o primeiro passo é calcular algumas propriedades geométricas da peça. Fazendo isso:

y c g = 222,368

Q m á x   a b a = 1,629 × 10 - 3

Q b = 1,10528 × 10 - 3

Vale ressaltar que caso você tenha dúvida em como calcular algum desses parâmetros, temos os capítulos deste assunto resolvidos, só dar uma olhada lá, aqui o foco é outro. Como o problema nos pede para mostrar que o momento de Inércia é o do enunciado:

I = 0,05 × 0,15 3 12 + 0,05 × 0,15 × 0,147 2 + 0,2 × 0,2 3 12 + 0,2 × 0,2 × 0,027 2 = 340,82 × 10 6

Agora, podemos calcular as tensões cisalhantes:

τ m á x = V Q m á x I t

τ b   a b a = V Q b I t

τ b   a l m a   = V Q b I t

Substituindo os valores nas fórmulas, teremos:

τ m á x = 4,18

τ b   a b a = 2,84

τ b   a l m a   = 11,35

Com estes dados, podemos determinar a distribuição pedida:

Passo 2

Para calcular a força pedida, devemos determinar o momento estático na área pedida, em função da altura:

Q = y + 0,2224 - y 2 0,2224 - y 0,05 = ( 1,2365 - 25 y ² ) 10 - 3  

Logo, a tensão em função de y será:

τ = V Q I t = 12,7 - 256,73 y 2

Como a força é a tensão integrada na superfície, teremos que:

F = ∫ τ d A = ∫ 0,0724 0,2224 12,7 - 256,73 y 2 10 - 6 0,5 d y = 49,78 k N

Resposta

F = 49,78 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de aço laminado mostrada na figura foi reforçada acrescentando-lhe duas placas 16 x 200 mm, usando parafusos de 18 mm de diâmetro espaçados longitudinalmente a cada 120 mm. Sabendo que a tensão
Uma coluna é fabricada conectando os perfis de aço laminado mostrados na figura porparafusos de diâmetro 3/4 pol. espaçado longitudinalmente a cada 5 pol. Determine a tensão de cisalhamento média nos
Uma viga consiste em três pranchas conectadas por parafusos de aço espaçados longitudinalmente de 225 mm conforme mostrado. Sabendo que a força cortante na viga é vertical e igual a 6 KN e que a tensã
Duas placas de aço de 12 x 220 mm de seção transversal retangular são soldadas a um perfil W250 x 58 como mostra a figura. Determine a maior força cortante vertical admissivel para que a tensão de cis
Uma viga consiste em cinco pranchas com seção transversal de 1,5 x 6 in. Conectadas por parafusos de aço espaçados longitudinalmente de 9 in. Sabendo que a força cortante na viga é vertical e igual a