Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 29b
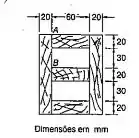
Várias pranchas são coladas juntas para formar a caixa mostrada. Sabendo-se que a viga é submetida a uma força cortante vertical de 3kN, determine a tensão de cisalhamento média na junta colada: (b) em B;
Passo 1
Geralmente é comum a gente começar o problema pelo cálculo do momento de inércia, porém quando o ponto de interesse for como o ponto B, próximo ao centro da peça, a dica é começar olhando pro momento estático.
Precisamos calcular o momento estático para encontrar o fluxo, pro ponto B o momento estático que nos interessa é da peça a direita da ligação no meio:
Com isso o fluxo de cisalhamento é:
A tensão de cisalhamento será então:
Resposta
(b)
Exercícios de Livros Relacionados
Selecione no Apêndice B a viga de aço de abas largas de menor peso e altura que suportará com segurança as cargas mostradas na figura, na qual w = 0 e P = 50k N . A tensão de flexão admissível é σ a d
Trace os diagramas de força cortante e momento fletor para a viga W310x21 e verifique se ela suportará com segurança a carga mostrada na figura. A tensão de flexão admissível é σ a d m = 160M P a e a
A viga simplesmente apoiada é composta por duas seções W310x33 montadas como mostra a figura. Determine a carga uniforme máxima w que ela suportará se a tensão de flexão admissível for σ a d m = 160M
Selecione no apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é σ a d m = 160M P a e atenção de cisalhamen
A viga será usada para suportar uma máquina que tem peso de 80k N e centro de gravidade em G. Se a tensão de flexão máxima não puder ultrapassar σ a d m = 160M P a , determine a largura b exigida para