A viga é composta por três tábuas coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a tensão de cisalhamento desenvolvida nas juntas coladas na seção a-a. Os apoios em C e D exercem somente reações verticais sobre a viga.
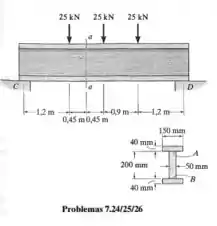
Passo 1
Falaaa! Isso é uma questão de cisalhamento em vigas compostas. Tem um passo a passo para resolver. Vem comigo que te mostro!
Vamos começar com as reações de apoio:
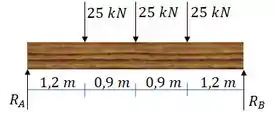
Como o carregamento e as reações são simétricos
Aplicando as equações de equilíbrio
Passo 2
Vamos fazer um corte na seção de interesse, e posicionar a componente do esforço cortante. Aí achamos ele pelas equações de equilíbrio.
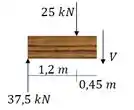
Aplicando as equações de equilíbrio:
Passo 3
Vamos calcular o momento de inércia de toda a seção:

A gente vai calcular o momento do retângulo todo. Diminuir esse retângulo e somar a alma da seção.
Passo 4
Vamos calcular o momento estático na junta. Para saber que área escolher é só cê imaginar que está segurando sua seção nessa aba de cima. Se a cola parar de funcionar, uma parte da seção cai, e outra fica na sua mão. Essa que ficou vai ser nossa área.
No nosso caso escolhemos aba de cima.
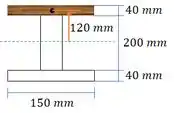
Passo 5
Agora aplicamos a equação do cisalhamento:
Substituindo os valores. Lembre-se que para encontrar a tensão máxima sobre uma junta, devemos usar a menor base,
Isso a gente calculou para a seção , mas vale o mesmo para a seção por causa da simetria, beleza?
Obs: Nessa questão o gabarito do livro tem um errinho, tá?