Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 13
O raio da haste de aço é 30 mm. Se ela for submetida a um cisalhamento V = 25 kN, determine a tensão de cisalhamento máxima.
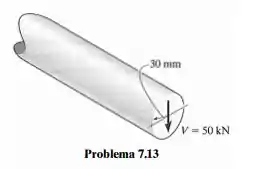
Passo 1
Pra começar, vamos dar uma olhada nas informações fornecidas pela questão:
Dados da questão:
A questão pede:
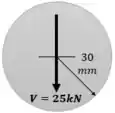
A questão pede a tensão de cisalhamento máxima, lembre-se que o ponto de maior tensão cisalhante ocorre na linha neutra da seção e essa tensão de cisalhamento máxima pode ser calculada com a equação:
A gente já tem a nossa força cisalhante V, e t é a espessura da seção no ponto de interesse. Nossa meta aqui é ir atrás do momento estático Q, e do momento de inércia I.
Passo 2
A primeira conta que vamos fazer é calcular o momento de inércia da figura:
Onde o momento de inércia de um círculo é tabelado:
Passo 3
Agora vamos pra parte mais complicada da questão. Calcular o momento estático!
A gente quer calcular a tensão máxima, e essa tensão irá ocorrer na linha neutra.
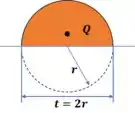
O nosso momento estático, ele é calculado do topo até o ponto onde queremos saber a tensão de cisalhamento, que nesse caso é qualquer ponto da linha neutra. Sendo assim, o nosso momento estático fica com essa cara aqui:
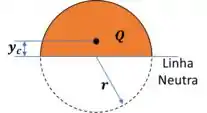
E para calcular esse momento estático , faremos:
Onde é a área de laranja ali e é a posição do centroide dessa área.
O centróide de uma semi-circunferencia é tabelado, e pode ser encontrado nas tabelas no final do livro e é dado por:
E a área da semi-circunferência é metade da área de um círculo:
Então agora temos tudo que é preciso para calcular o momento estático da semi-circunferência:
Rearrumando temos:
E enfim
Passo 4
Por ultimo vamos lembrar que t é a espessura da peça onde a gente quer encontrar a tensão e lembrando que a é no meio, na linha neutra, temos.
Daí voltamos pra nossa fórmula:
Para esse caso,
Substituindo os valores temos:
E como .
Chegamos em:
E já sabemos que