Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 54
Resolver problema. 1.53, assumindo que os pinos em C e F foram substituídos por pinos com diâmetro de 30 mm
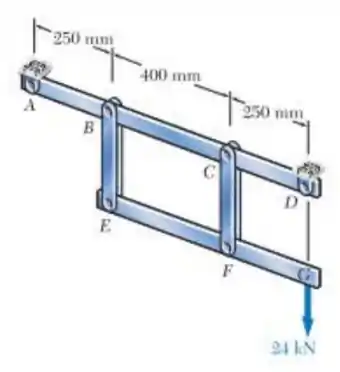
Passo 1
E ai gurizada tudo belezinha??? Primeiramente vamos desenhar diagrama do corpo livre para termos uma ideia do comportamento :D
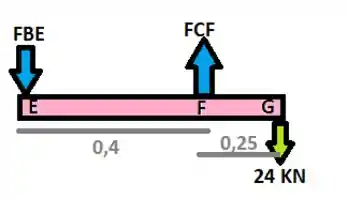
Primeiramente vamos realizar o somatório do momento em E , vem comigo :D
Baseado na tensão nos VÍNCULOS CF
Com base no cisalhamento duplo nos pinos
Passo 2
O fator de segurança pode ser calculado da seguinte maneira:
Resposta
Exercícios de Livros Relacionados
Dois elementos de madeira mostrados suportam uma carga de 16 kN e são unidos por juntas de madeira contraplacadas perfeitamente coladas pelas superfícies de contato. A tensão de cisalhamento limite da
Em um projeto alternativo para a estrutura do Problema 1.55, deve ser utilizado um pino de 10 mm de diâmetro em A. Supondo que todas as outras especificações permaneçam inalteradas, determine a carga
O elemento ABC, suportado por um pino em C e por um cabo BD, foi projetado para suportar uma carga P de 16 kN conforme mostrado. Sabendo que a carga limite para o cabo BD é de 100 kN, determine o coef
Duas placas de aço são mantidas juntas através de parafusos de aço de alta resistência com 16 mm de diâmetro perfeitamente ajustados no interior de espaçadores cilíndricos de latão. Sabendo que a tens
Na estrutura de aço mostrada na figura é utilizado um pino de 6 mm de diâmetro em C e são utilizados pinos de 10 mm de diâmetro em B e D. O limite da tensão de cisalhamento é 150 MPa em todas as conex