Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 53

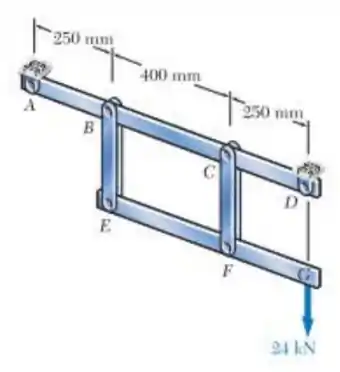
Cada um dos dois elos verticais CF que conectam os dois montantes horizontais AD e EG possui uma seção transversal retangular uniforme de 10 x 40 mm e é fabricado em aço com uma força máxima na tensão de 400 MPa, enquanto cada um dos pinos em C e F têm um diâmetro de 20 mm e são fabricados em aço com uma resistência máxima ao cisalhamento de 150 MPa. Determine o fator de segurança global para os vínculos CF e os pinos que os conectam aos elementos horizontais.

Passo 1

E ai gurizada tudo belezinha??? Primeiramente vamos desenhar diagrama do corpo livre para termos uma ideia do comportamento :D

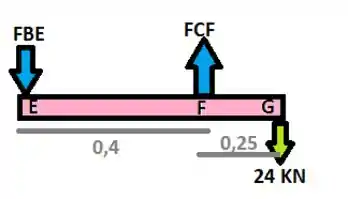
Primeiramente vamos realizar o somatório do momento em E , vem comigo :D

+ ↺ ∑ M E = F × d = 0

0,4   F C F - 0,65 × 24 × 10 3 = 0

F C F = 39 × 10 3 N

Baseado na tensão nos VÍNCULOS CF

A = B - D T = 0,04 - - 0,02 × 0,01 = 200 × 10 - 6   m ²

F u = 2 σ A = 2 × 400 × 10 6 200 × 10 - 6 = 160 × 10 ³ N

Com base no cisalhamento duplo nos pinos

A = π 4 × d 2 = π 4 × 0,02 2 = 314,16 × 10 - 6   m ²

F u =   2 σ A = 2 × 150 × 10 6 × 314,16 ×   10 6 = 94,25   × 10 3  

Passo 2

O fator de segurança pode ser calculado da seguinte maneira:

F S = F u F C F = 94,25   × 10 3 39 × 10 3 = 2,42

Resposta

2,42

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os elementos AB e BC da treliça mostrada são feitos da mesma liga. Sabe-se que uma barra quadrada de 20 mm de lado feita do mesmo material foi ensaiada até falha e que uma carga final de 120 kN foi re
O vínculo AB deve ser feito de aço para o qual a tensão normal é de 450 MPa. Determine a área da seção transversal da AB para a qual o fator de segurança será 3,50. Suponha que o vínculo seja reforçad
Três parafusos de aço com 18mm de diâmetro devem ser utilizados para fixar a chapa de aço mostrada na figura viga de madeira. Sabendo que a chapa suportará uma carga P =110 KN e que a tensão de cisalh
Para a conexeão e carregamento de Prob. 1,43, determine o coeficiente de segurança, sabendo que o comprimento de cada junta é L=180 m180 m
Uma plataforma de 40 kg está presa à extremidade B de uma barra AB de madeira, de 50 kg, suportada, conforme mostra a figura, por um pino em A e por uma barra esbelta de aço BC com um limite de carga