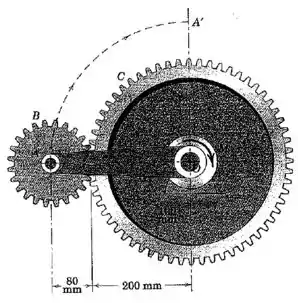
A respeito do conjunto apresentado, o braço possui uma massa de e um raio de giração em relação a de . A engrenagem tem uma massa de e pode ser tratada como um disco circular maciço. A engrenagem está fixa no plano vertical e não pode girar. Se um momento constante é aplicado ao braço , inicialmente em repouso na posição horizontal mostrada, calcule a velocidade do ponto quando atinge o topo em .

Agora vamos procurar uma expressão para a variação de energia cinética entre o ponto inicial e o ponto :

O braço tem apenas movimento de rotação em torno do seu eixo em :

Já a engreagem tem movimento de rotação em torno do seu próprio centro e movimento de translação ao longo da engrenagem com velocidade .

Agora uma informação importante: A velocidade do centro de massa de , e da extremidade do braço são iguais. Podemos deduzir isso pela forma como eles estão conectados.

E é justamente essa velocidade que queremos calcular. Podemos usar essa igualdade para escrever o seguinte:

Então:

Para completar essa equação, vamos encontrar os momentos de inércia e substiuir os valores que foram dados.

Começando pelo momento de inércia do braço em torno do ponto :

E o momento de inércia da engrenagem em torno do seu centro de massa:

Substituindo esses e os outros valores na nossa expressão, encontramos o seguinte:

Agora vamos procurar uma expressão para a variação de energia potencial gravitacional:

Vamos colocar o zero da nossa energia potencial na altura do ponto .

A distância entre e o centro de massa do braço é:

Então quando o braço passa da posição inicial (horizontal) para a final (vertical), a variação de altura do centro de massa do braço é:

Já o centro de massa da engrenagem sobe uma altura igual ao raio da engrenagem somado ao seu próprio raio:

Então:

Por fim, vamos voltar à nossa lei de conservação de energia: