Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 87

Quando o motor tem sua velocidade gradualmente elevada, uma oscilação vibratória muito grande de todo o motor em torno de O - O ocorre a uma velocidade de 360   r p m , o que mostra que essa velocidade corresponde à frequência natural de oscilação livre do motor. Se o motor possui uma massa de 43   k g e um raio de giração de 100   m m em relação a O - O , determine a rigidez k de cada um dos quatro suportes de molas idênticas.

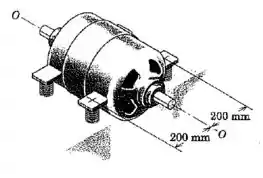
Passo 1

Vamos montar uma equação de momentos em torno do eixo O - O :

∑ M O = I O θ ¨

O momento de inércia pode ser calculado através do raio de giração k O que foi dado no enunciado:

I O = m k O 2

E o único momento que vai afetar a oscilação do motor em relação a esse eixo é produzido pelas molas conforme o motor se inclina por um ângulo θ :

F = k Δ x = k 0,2 sen ⁡ θ

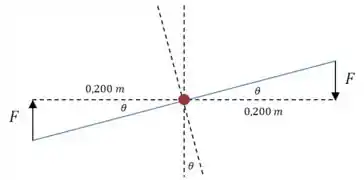
E a distância perpendicular entre essas forças e o ponto O é:

d = 0,2 cos ⁡ θ

Então, considerando que temos um total de 4 molas:

∑ M O = - 4 k 0,2 2 sen ⁡ θ cos ⁡ θ

Passo 2

Vamos substituir tudo isso na nossa equação principal:

∑ M O = I O θ ¨

- 4 k 0,2 2 sen ⁡ θ cos ⁡ θ = m k O 2 θ ¨

E podemos aproximar sen ⁡ θ ≅ θ e cos ⁡ θ = 1 :

- 0,16 k θ = m k O 2 θ ¨

Então:

θ ¨ + 0,16 k m k O 2 θ = 0

Portanto, a frequência angular de oscilação é:

ω 2 = 0,1 6 k m k O 2 = ( 0,16 ) 43 0,1 2 = 0,372   k

ω = 0,372 k

Passo 3

Nós queremos achar o valor da constante k que permite uma velocidade angular de 360   r p m :

ω = 360   r p m = 360 2 π ( 60 )   r a d / s

ω = 37,70   r a d / s

Então:

37,70 = 0,372 k

k = 3820   N / m

Resposta

A rigidez de cada um dos suportes é k = 3820   N / m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro de 1000 k g com quatro ocupantes de 82 k g viaja em uma estrada de terra com “costelas” separadas por uma distância média de 4,0 m . O carro trepida com amplitude máxima quando está a 16 k m
A haste uniforme de comprimento l e massa m está suspensa em seu ponto médio por um arame de comprimento L . A resistência do arame à torção é proporcional ao seu ângulo de rotação θ e é igual a ( J G
A casca cilíndrive com paredes finas de raio r e altura h é soldada ao pequeno eixo em sua extremidade superior conforme indicado. Determine a frequência circular natural ω n para pequenas oscilações
Uma placa retangular uniforme é articulada em torno de um eixo horizontal que atravessa um de seus vértices conforme mostrado. Determine a frequência natural ω n para pequenas oscilações.
Desenvolva a equação diferencial para pequenas oscilações do pêndulo sob a ação das molas e determine o período τ . A posição de equilíbrio é vertical como indicada. A massa da haste é desprezível.