Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 68
A roda de 150 kg tem um raio de giração em relação a seu centro de massa O de = 250 mm. Se ela gira no sentido anti-horário com uma velocidade angular = 1200 rev/min no instante em que as forças de tração = 2000 N e = 1000 N são aplicadas a fita do freio em A e B, determine o tempo necessário para parar a roda.
Passo 1
Vamos considerar a aceleração da gravidade como .
Iniciaremos o exercício calculando o momento de inércia da roda em relação ao seu centro:
Com isso, podemos aplicar o somatório de momentos em torno de O com o auxílio da figura a seguir:
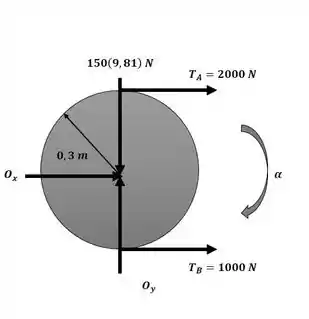
Passo 2
Antes de aplicarmos a equação da velocidade angular, devemos converter a velocidade angular fornecida no enunciado para rad/s:
Passo 3
Agora, podemos aplicar a equação da velocidade angular para o sistema:
Resposta
Exercícios de Livros Relacionados
125. Os dois cones circulares retos homogêneos maciços, cada um de massa m , são fixados um ao outro em seus vértices para formar uma unidade rígida e estão girando em torno de seu eixo de simetria ra
124. O satélite de observação da Terra está em uma órbita circular de período τ . A velocidade angular do satélite em torno de seu eixo y ou eixo de arfagem é ω = 2 π / τ , e as velocidades angulares
128. Se o navio do Exemplo 7 / 8 está em curso reto, mas a sua proa está abaixando enquanto cai no vale de uma onda, determine o sentido do momento giroscópico exercido pelo rotor da turbina sobre a e
129. Um carro experimental é equipado com um estabilizador giroscópico para neutralizar completamente a tendência do carro a inclinar ao realizar uma curva (sem variação na força normal entre os pneus
127. A casca cilíndrica está girando no espaço em torno de seu eixo geométrico. Se o eixo sofre uma ligeira oscilação, para quais razões de l / r o movimento será de precessão direta ou retrógrada?