129. Um carro experimental é equipado com um estabilizador giroscópico para neutralizar completamente a tendência do carro a inclinar ao realizar uma curva (sem variação na força normal entre os pneus e a pista). O rotor do giroscópico possui uma massa e um raio de giração , e está montado em mancais fixos sobre um eixo que é paralelo ao eixo traseiro do carro. O centro de massa do veículo está a uma distância acima da pista, e o carro está contornando uma curva horizontal sem inclinação lateral a uma velocidade . A que velocidade o rotor deve girar e em que sentido , para neutralizar completamente a tendência do carro a capotar, tanto para uma curva à direita como à esquerda? A massa combinada do carro e do rotor é .
Passo 1
Bom, primeiro vamos considerar uma curva à direita e esquematizar como fica o rotor nessa situação:
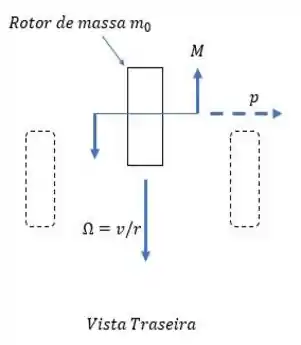
Passo 2
Com isso, podemos analisar como o rotor atua no carro em uma curva à direita:
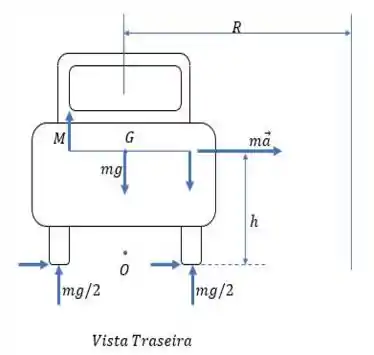
Passo 3
Como sabemos que o carro está em uma curva e há apenas a força , sabemos que ela deve ser igualada à força centrípeta:
Passo 4
Se fizermos agora o somatório de momentos em relação ao ponto :
E do passo anterior, temos:
Passo 5
Porém, sabemos que o momento do rotor é dado por:
Para o momento de inércia , nós temos a relação:
E para frequência angular :
Portanto, se igualarmos ambos momentos encontrados e substituir as variáveis:
Isolando :
Resposta
A velocidade que o rotor deve girar deve ser de:
E a direção deve ser oposta à rotação das rodas.