Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 127

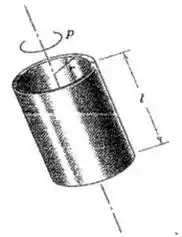
127. A casca cilíndrica está girando no espaço em torno de seu eixo geométrico. Se o eixo sofre uma ligeira oscilação, para quais razões de l / r o movimento será de precessão direta ou retrógrada?

Passo 1

Bom, primeiro a gente vai esquematizar a casca cilíndrica:

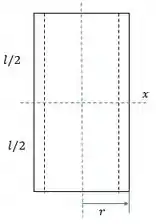
Passo 2

Agora, vamos calcular os momentos de inércia I e I 0 para verificar a razão I 0 / I , onde:

I = I z z

E

I 0 = I x x

Para o valor de I dado por:

I = m r 2

Já para I 0 , precisaremos usar o teorema dos eixos paralelos:

I 0 = 1 2 m r 2 + 1 12 m l 2

I 0 I = 1 2 m r 2 + 1 6 l 2 m r 2

I 0 I = 1 2 m r 2 m r 2 + 1 12 m l 2 m r 2

I 0 I = 1 2 + 1 12 l r 2

Passo 3

Para termos uma precessão direta a razão I 0 / I deve ser maior que 1 :

I 0 I > 1 → 1 2 + 1 12 l r 2 > 1

1 12 l r 2 > 1 2

l r 2 > 12 2

l r > 6

Passo 4

Já para termos uma precessão retrógrada, a razão I 0 / I deve ser menor que 1 :

I 0 I < 1 → 1 2 + 1 12 l r 2 < 1

1 12 l r 2 < 1 2

l r 2 < 12 2

l r < 6

Resposta

Razão l / r para uma precessão direta:

l r > 6

Razão l / r para uma precessão retrógrada:

l r < 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

112. A estrutura principal de uma proposta de estação espacial consiste em cinco cascas esféricas conectadas por raios tubulares. O momento de inércia da estrutura em relação ao seu eixo geométrico A
108. A figura mostra um giroscópio montado com um eixo vertical e utilizado para estabilizar um navio hospital contra o balanço. O motor A gira o pinhão que produz a precessão do giroscópio pela rotaç
107. O pião de 12g de raio de giração em relação ao seu eixo de giro de 16m m está girando à taxa p = 3600r p m no sentido indicado, com seu eixo de giro fazendo um ângulo θ = 20 ° com a vertical. A d
121. A barra retangular está girando no espaço em torno de seu eixo longitudinal à taxa p = 200r p m . Se seu eixo oscila através de um ângulo total de 20 ° conforme mostrado, calcule o período τ da o
119. Um menino lança um disco circular fino (como um F r i s b e e ) com uma velocidade de giro de 300r p m . Observa-se o plano do disco oscilar através de um ângulo total de 10 ° . Calcule o período