Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 33
Efetue um cálculo no computador para um objeto se movimentando verticalmente no ar sob a ação da gravidade e sujeito a uma força de retardo proporcional ao quadrado da velocidade do objeto (veja a Equação 2.21). Use as variáveis para massa e para 0 raio do objeto. Todos os objetos são liberados em queda da cobertura de um edifício com de altura. Use um valor de e gere gráficos no computador para altura , velocidade e aceleração versus sob as condições a seguir e responda às questões:
(a) Uma bola de beisebol de massa e raio .
(b) Uma bola de pingue-pongue de massa e raio .
(c) Uma gota de chuva de raio .
(d) Todos os objetos alcançam suas velocidades terminais? Discuta os valores das velocidades ter- minais e explique suas diferenças.
(e) Por que uma bola de beisebol pode ser lançada mais longe do que uma bola de pingue-pongue, mesmo com a bola de beisebol tendo uma massa maior?
(f) Discuta as velocidades terminais de gotas de chuva grandes e pequenas. Quais serão as velocidades terminais de gotas de chuva com raios e ?
Passo 1
Faala meu povo, bora com tudo pra mais uma questão do nosso livro!
Letra (a)
Primeiramente para o item a, temos que a equação de Prandtl para a resistência do ar, nos dá:
Onde é o coeficiente de arrasto adimensional, é a densidade do ar, é a velocidade e é a área da seção transversal do objeto medida perpendicularmente à velocidade. Mas , então:
A força resultante na direção é igual à força da gravidade subtraída da força de resistência do ar:
Rearranjando a equação, temos:
Onde é a velocidade terminal. Agora precisamos plotar essas funções, com condições iniciais de e . O procedimento será o seguinte:
- Divida o intervalo de tempo em pequenos períodos .
- Encontre a velocidade após a partir da velocidade inicial.
- Multiplicamos a aceleração por um pequeno intervalo de tempo e adicione-o à velocidade anterior.
- Finalmente multiplicamos a velocidade por e adicione-o à posição anterior.
Agora vamos iniciar nosso item (a), para uma bola de baseball de e raio , a área é:
Usando um código em python ilustrado abaixo, iremos plotar os gráficos.
Passo 2
Letra (b)
Agora para nosso item (b), para uma bola de pingue-pongue de e raio , a área é:
Os gráficos são mostrados na figura a seguir:
Passo 3
Letra (c)
Para uma gota de chuva com raio de , a massa é igual ao volume dessa gota multiplicado pela densidade da água, ou seja:
A área, portanto, é:
Os gráficos são mostrados na figura a seguir:
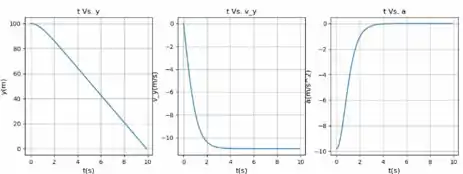
Passo 4
Letra (d)
Tomando como densidade do ar, as velocidades terminais são (a) , (b) e (c) para a bola de beisebol, pingue-pongue e gota de chuva, respectivamente. Tanto a bola de pingue-pongue quanto a gota de chuva essencialmente atingem suas velocidades terminais no momento em que atinge o solo. Se nós reescrevermos a massa como densidade média vezes volume, então descobrimos que . A diferenças nas velocidades terminais dos três objetos podem ser explicadas em termos de suas densidades e tamanhos.
Passo 5
Letra (e)
Nossa equação diferencial mostra que o efeito da resistência do ar é uma aceleração que é inversamente proporcional ao quadrado da velocidade terminal. Como a bola de beisebol tem uma maior velocidade terminal do que a bola de pingue-pongue, a magnitude de sua desaceleração é menor para uma dada velocidade. Se uma pessoa lança os dois objetos com a mesma velocidade inicial, a bola de beisebol vai mais longe porque tem menos arrasto.
Passo 6
Letra (f)
Da parte (e) vemos que a velocidade terminal é proporcional à raiz quadrada da densidade do material multiplicada pelo raio da gota, já que ambas as gotas têm a mesma densidade do material, então:
Para e , nós temos: