Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 37

Se as rodas traseiras da empilhadeira fornecerem uma força de tração combinada de F A = 1500   N , determine a sua aceleração e as reações normais sobre os pares de rodas traseiras e dianteiras. A empilhadeira tem uma massa de 1000 kg, com centro de gravidade em G 1 , e a carga pesa 4500 N , com centro de gravidade em G 2 . As rodas dianteiras estão livres para rodar. Despreze o peso das rodas.

Passo 1

Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².

Esquema para análise do sistema:

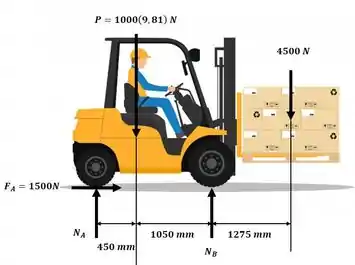
A aceleração da empilhadeira pode ser obtida através do somatório de forças no eixo x:

+ ← ∑ F x = m a G x

1500 = 1000 a G + 4500 9,81 a G

a G = 1,028   m / s 2

Passo 2

Usando o resultado obtido no passo 1 e escrevendo o somatório de momentos em relação ao ponto A, podemos extrair a reação normal em B:

↺ + ∑ M A = M k A

N B 1,5 - 1000 9,81 0,45 - 4500 2,775 = - 1000 1,028 0,6 - 4500 9,81 ( 1,028 ) ( 0,975 )

N B = 10556,11   N

Passo 3

Agora, podemos fazer o somatório de forças no eixo y e determinar a força de reação em A:

+ ↑ ∑ F y = m a G y

N A + 10556,11 - 1000 ( 9,81 ) - 4500 = 0

N A = 3753,89   N

Resposta

a G = 1,028   m / s 2

N A = 3753,89   N

N B = 10556,11   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia em relação ao eixo x e expresse o resultado em termos da massa total m do paraboloide. O materia
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o raio de giração k x . A densidade do material é ρ = 5 Mg/m3.
Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do semielipsoide.
Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do sólido.
O pêndulo consiste de uma placa tendo uma massa de 6kg e uma barra fina tendo uma massa de 2kg. Determine o raio de giração do pêndulo em relação a um eixo perpendicular à página e passando pelo ponto