Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 42
A caixa uniforme tem uma massa de 50 kg e repousa sobre o carrinho tendo uma superfície inclinada. Determine a menor aceleração que vai fazer com que a caixa tombe ou deslize em relação ao carrinho. Qual é a intensidade dessa aceleração? O coeficiente de atrito estático entre a caixa e o carrinho é .
Passo 1
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Vamos assumir inicialmente que a caixa irá deslizar sobre a superfície, logo, a força de atrito é dada por:
Sendo assim, podemos aplicar os somatórios de momento e de forças no sistema. Para facilitar os cálculos e a análise, o somatório de forças será feito no eixo x’ e y’ inclinados de 15° cada, para que fiquem na direção e normal, respectivamente, à superfície inclinada, conforme a figura que segue:
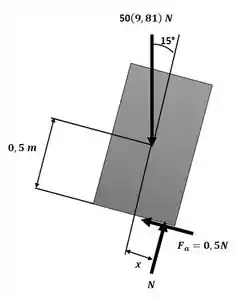
Passo 2
O somatório de momento será aplicado em torno de um ponto A (que será o ponto de apoio da caixa) a partir de uma distância x (ainda desconhecida) do centro da caixa,
Agora, aplicaremos o somatório de forças nos eixos x’ e y’:
Passo 3
Agora, resolveremos o sistema de equações isolando N da terceira equação e substituindo na segunda equação do passo 2, obtemos:
Agora, substituindo o valor da aceleração na primeira equação, obtemos o valor de x:
Portanto, como x