Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 38
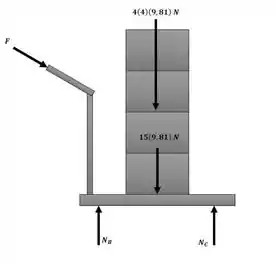
Cada caixa uniforme na pilha de quatro caixas tem uma massa de 4 kg. A pilha está sendo transportada em um carrinho que tem uma massa de 15 kg. Determine a força máxima F que a mulher pode exercer sobre o carrinho na direção mostrada de maneira que nenhuma caixa na pilha tombe ou deslize. O coeficiente de atrito estático em todos os pontos de contato é . As rodas do carrinho estão livres para rodar. Despreze sua massa.
Passo 1
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Assumiremos que a caixa é simétrica e uniforme, para que seu centro de massa esteja exatamente no meio dela e possamos considerar as quatro caixas como um só corpo.
Consideraremos também um ponto de apoio somente na quina esquerda da caixa inferior (ponto A), para que possamos simular o caso em que a pilha esteja na iminência de tombar. A situação está ilustrada na figura a seguir:
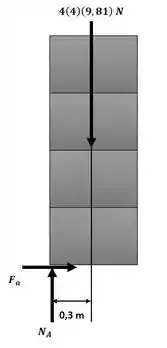
Sendo assim, podemos aplicar somatório de momentos em torno do ponto A:
Passo 2
Podemos também, aplicar somatório de forças em torno do eixo y para encontrar e do eixo x para encontrar a força de atrito real exercida na superfície entre a caixa inferior e o carrinho, respectivamente:
Temos que a força de atrito máxima é dada por:
Sendo assim, como a força de atrito real é menor do que a força de atrito estático máxima, o carrinho e a pilha de caixas se movimentam como um só corpo.
Passo 3
Agora, que já sabemos que a pilha de caixas e o carrinho podem ser analisados juntos, podemos aplicar o somatório de forças no eixo x nesse sistema conforme a figura 2:
