Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 29

A roseta de deformação a 60° está montada sobre uma viga. As seguintes leituras foram obtidas para cada extensômero: ∈ a = - 780 × 10 - 6 ;   ∈ b = 400 × 10 - 6   e ∈ c = 500 × 10 - 6 .   Determine (a) as deformações principais no plano e (b) a deformação por cisalhamento máxima no plano e a deformação normal média. Em cada caso, mostre o

elemento distorcido devido a essas deformações.

Passo 1

Fala aí pessoal. O problema quer que a gente determine as deformações principais no plano, então vamos lá. Sabemos que:

∈ c = ∈ x c o s ⁡ ² ( θ c ) + ∈ y s e n 2 θ c + γ x y s e n θ c c o s ⁡ ( θ c )

∈ a = ∈ x c o s ⁡ ² ( θ a ) + ∈ y s e n 2 θ a + γ x y s e n θ a c o s ⁡ ( θ a )

∈ b = ∈ x c o s ⁡ ² ( θ b ) + ∈ y s e n 2 θ b + γ x y s e n θ b c o s ⁡ ( θ b )

Substituindo as tensões fornecidas pelo problema e os ângulos, ficaremos com um sistema de 3 equações e 3 incógnitas. Como não é o nosso foco aqui, vou colocar os valores obtidos pela resolução do sistema:

∈ x = - 780 × 10 - 6

∈ y = - 860 × 10 - 6

γ x y = - 115,47 × 10 - 6

O próximo passo é calcular as deformações principais através da fórmula:

∈ 1,2 = ∈ x + ∈ y 2 ± ∈ x - ∈ y 2 2 + γ x y 2 2

Substituindo, ficamos com:

∈ 1 = 862 × 10 - 6

∈ 2 = - 782 × 10 - 6

A orientação será dada por:

t g 2 θ = 57,74 820 = 0,07041

Logo, teremos:

θ 1 = 2,01 °

θ 2 = 2,01 ° - 90 ° = - 88 °

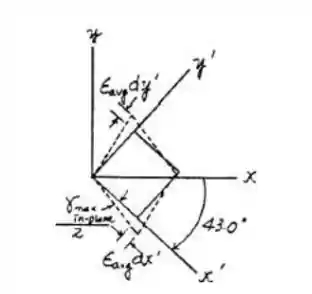
Mostrando o elemento, teremos:

Passo 2

Na letra b, ele nos pede a deformação por cisalhamento máxima e a deformação média associada. Logo, teremos:

γ m á x = - 2 R = - 1 644 × 10 - 6

∈ m é d = ∈ x + ∈ y 2 = 40 × 10 - 6

Já a orientação, será dada por:

2 θ = 90 - 2 θ 1

Logo:

θ = 43 °

O elemento ficará da seguinte forma:

Resposta

  1. ∈ 1 = 517 × 10 - 6

    ∈ 2 = - 420 × 10 - 6

    θ 1 = 2,01 °

    θ 2 = - 88 °

γ m á x = - 2 R = - 1 644 × 10 - 6

∈ m é d = ∈ x + ∈ y 2 = 40 × 10 - 6

θ = 43 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o dado estado plano de deformação, usar o método da S e c .6.10 para determinar o estado de deformação associado aos eixos x ’ e y ’ , que foram girados de um ângulo θ , no sentido mostrado. ε x
Para o estado plano de tensões mostrados, determinar:Os planos principais As tensões principaisA máxima tensão de cisalhamento.
Para o estado plano de tensões mostrados, determinar:Os planos principais As tensões principaisA máxima tensão de cisalhamento.
Para a barra do P r o b . 6.150 , e sabendo-se que o aço usado E = 200G P a e ϑ = 0,30 , determinar as três deformações especificas principais e a máxima deformação especifica de cisalhamento, no pont
As fibras de uma peça de madeira formam um ângulo de 15° com a vertical. Para o estado plano de tensões mostrado, determinar:A tensão de cisalhamento, no plano, paralelo as fibras;A tensão normal perp