Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 132
Sabendo que o coeficiente de atrito entre o bloco de e o plano inclinado é , determine o menor valor de necessário para iniciar o movimento no plano inclinado, o valor correspondente de .
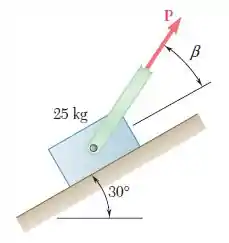
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Observe o diagrama abaixo:
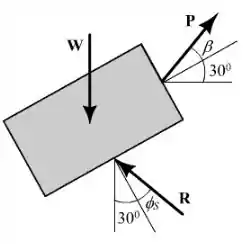
O ângulo de atrito é dado por:
Substituindo , temos:
Sabemos também que:
Passo 2
Para o valor mínimo de , temos que deve ser perpendicular a . Portanto:
Substituindo, temos:
Resolvendo, temos que:
Passo 3
Analisando geometricamente, temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
O gancho por atrito é composto de uma estrutura fixa e de um cilindro de peso desprezível. Um pedaço de papel é colocado entre a parede e o cilindro. Se θ=20 º º, determine o menor coeficiente de atri
O disco tem peso W e encontra-se em um plano que possui coeficiente de atrito estático m. Determine a maior altura h à qual o plano pode ser elevado sem fazer com que o disco deslize.
O semicilindro homogêneo tem massa de 20k g e centro de massa em G. Se a força P é aplicada na borda, e r=300m m , determine o ângulo θ quando o semicilindro está na iminência de deslizamento. O coefi
Determine o maior ângulo θ de modo que a escada não deslize quando um homem de 75 kg estiver na posição mostrada. A superfície é um tanto escorregadia, onde o coeficiente de atrito estático em A e
A viga AB tem massa e espessura desprezíveis e suporta o bloco uniforme de 200k g . Ela é apoiada em A por um pino e, na outra ponta, por um poste com massa de 20k g e espessura desprezível. Determine