Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 129

Determine a aceleração angular do segmento AB se o segmento CD tem a velocidade angular e desaceleração angular mostradas.

Passo 1

Começaremos o exercício analisando o diagrama a seguir:

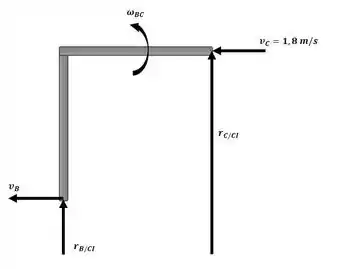
Como CI está no infinito, então:

ω B C = 0

Passo 2

Agora iremos encontrar os valores de interesse para aplicar a equação da aceleração com o auxílio da imagem a seguir:

v B = v C = 0,9 2 = 1,8   m / s

a C n = 2 2 0,9 = 3,6   m / s 2   ↓

a C t = 4 0,9 = 3,6   m / s 2   →

a B n = 1,8 2 0,3 = 10,8   m / s 2   ↓

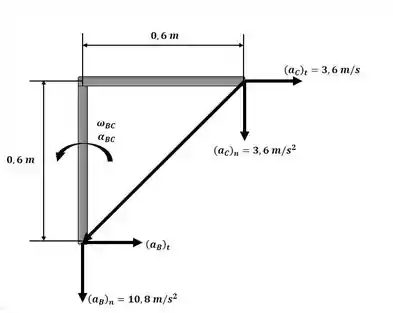
Passo 3

Agora iremos aplicar a equação da aceleração para os pontos B e C:

a → B = a → C + α B C × r → B / C - ω B C 2 r → B / C

a B t i → - 10,8 j → = 3,6 i → - 3,6 j → + α B C k → × - 0,6 i → - 0,6 j → - 0

Agora, igualando os componentes:

+ ↑ - 10,8 = - 3,6 - 0,6 α B C → α B C = 12   r a d / s 2

+ →   a B t = 3,6 + 0,6 α B C → a B t = 10,8   m / s 2

Sendo assim:

α A B = 10,8 0,3 → α A B = 36   r a d / s 2

Resposta

α A B = 36   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra AO possui uma velocidade angular constanteω no sentido anti-horário durante um curto intervalo de seu movimento. Para a posição mostrada determine as acelerações angulares de AB e BC.
O mecanismo do Prob.5/75 é reapresentado aqui. Cada uma das barras deslizantes A e B se acopla sem deslizar na sua respectiva borda das duas rodas rebitadas. Se, além da informação apresentada, a barr
No instante representado, θ = 45 ° e a placa triangular ABC possui uma velocidade angular no sentido anti-horário de 20 rad/s e uma aceleração angular no sentido horário de 100 rad/s². Determine os mó
O movimento plano da placa triangular ABC é controlado pela manivela AO e pela barra DB. Para o instante representado, quando AO e DB são verticais, AO possui uma velocidade angular no sentido horário
A placa triangular, reapresentada aqui a partir do Prob. 5/76, possui uma velocidade angular no sentido horário de 3 rad/s e AO possui aceleração angular nula para o instante representado. Determine a