Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 133

O flutuador de ponta de asa retrátil é utilizado em avião capaz de pousar na água. Determine as acelerações angulars α C D , α B D e α A B no instante mostrado se a luva roscada C se desloca ao longo do parafuso rotativo horizontal com uma aeleração α C = 0,15   m / s 2 . Na posição mostrada, v C = 0 . Além disso, os pontos A e E estão conectadas por pinos à asa e os pontos A e C são coincidentes no instante mostrado.

Passo 1

Começaremos o exercício analisando as velocidades em alguns pontos de interesse. Como v C = 0 , então:

ω C D = 0

E, dessa forma, podemos afirmar também que:

ω B D = ω A B = ω E D = 0

Agora podemos aplicar a equação da aceleração para o braço ED e obter a aceleração no ponto D com o auxílio da figura a seguir:

a → D = a → A + α E D × r → E D - ω E D 2 r → E D

a → D = α E D k → × - 0,424 i → - 0,424 j → - 0

a → D = 0,424 α E D i → - 0,424 α E D j →   m / s 2

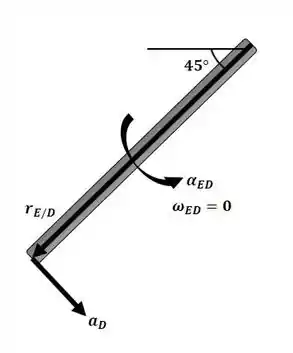
Passo 2

A aceleração do ponto B pode ser obtida analisando o braço AB conforme a figura a seguir:

a → B = α A B × r → B / A - ω A B 2 r → B / A

a → B = α A B k → × - 0,848 j → - 0

a → B = 0,848 α A B i →   m / s 2

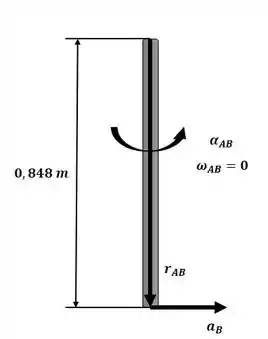
Agora iremos aplicar a equação da aceleração para o braço CD conforme a figura a seguir:

a → D = a → C + α C D × r → D / C - ω C D 2 r → D / C

0,424 α E D i → - 0,424 α E D j → = - 0,15 i → + α C D k → × 0,424 i → - 0,424 j → - 0

0,424 α E D i → - 0,424 α E D j → = 1,414 α C D - 0,15 i → + 0,424 α C D j →

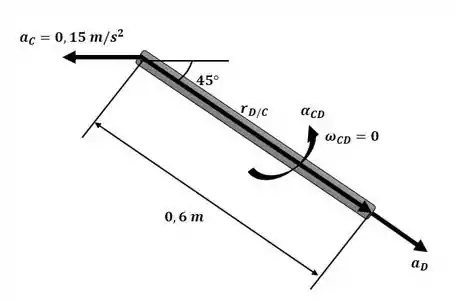
Igualando as componentes i e j, temos:

- 0,424 α E D = 0,424 α C D → a E D = - α C D

0,424 α E D = 0,424 α C D - 0,15 → 0,424 - α C D = 0,424 α C D - 0,15

α C D = 0,177   r a d / s 2

Passo 3

Agora iremos analisar o braço BD conforme a figura a seguir e aplicar a equação da aceleração:

a B = a D + α B D × r B / D - ω B D 2 r B / D

0,848 α A B i = - 0,0750 i + 0,0750 j + α B D k × - 0,424 i - 0,424 j - 0

0,848 α A B i = 0,424 α B D - 0,075 i + 0,075 - 0,424 α B D j

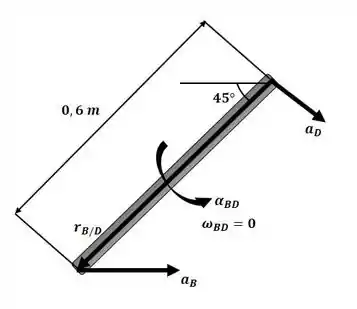
Agora, igualando os componentes:

0 = 0,075 - 0,424 α B D → α B D = 0,177   r a d / s 2

0,848 α A B = 0,424 α B D - 0,075 → α A B = 0   r a d / s 2

Resposta

α C D = 0,177   r a d / s 2

α B D = 0,177   r a d / s 2

α A B = 0   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a aceleração do pistão do Exemplo 5/15 para (a) θ = 0 ° ,b θ = 90 °ec θ = 180 ° . Considere o sentido positivo da direção x para a direita.
A configuração mostrada é projetada para produzir a oscilação do recipiente de pequenas peças em torno de C, como parte de um processo de produção. Obtenha uma expressão para a aceleração angular α do
A carga P é abaixada pelas duas polias que estão presas uma a outra e giram como um só conjunto. Para o instante representado, o tambor A possui uma velocidade angular no sentido anti-horário de 4 rad
Calcule a aceleração angular da placa na posição mostrada, onde a barra de controle AO possui uma velocidade angular constante ω O A = 4 r a d s eθ = 60 ° para ambas as barras.
A barra AB do Prob. 5/72 é reapresentada aqui. Se a velocidade do ponto A é de 3 m/s para a direita e é constante para um intervalo incluindo a posição mostrada, determine a aceleração tangencial do p