Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 99
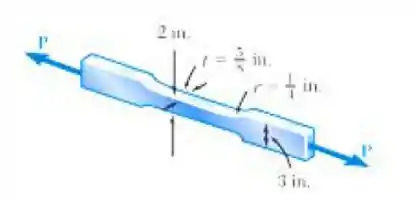
(a) sabendo que a tensão admissível é de , determine a intensidade máxima admissível de carga centrada P, (b) determine a mudança percentual da intensidade máxima admissível de P se as porções salientes das extremidades do corpo de prova são removidas.
Passo 1
E ai gurizada tudo belezinha? O enunciado pede para que a gente determine a intensidade máxima admissível e a mudança percentual da intensidade máxima admissível, considerando a relação dos diâmetros temos:
Agora precisamos determinar a área:
Considerando podemos determinar a força P :D
E agora a mudança percentual da intensidade, considernado
Resposta
Exercícios de Livros Relacionados
Sabendo-se que a haste de ligação BD tem uma seção transversal uniforme, de área igual a 800m m ² ², determine a intensidade da carga P para que a tensão normal na haste BD seja 50M P a .
Uma haste de ligação AC tem uma seção transversal retangular uniforme de 3,2 mm de espessura e 25,4 mm de largura. Determine a tensão normal na porção central da haste, quando α = 0 ° .
Sabendo-se que a haste de ligação BD tem uma seção transversal uniforme, de área igual a 800m m ² ², determine a intensidade da carga P para que a tensão normal na haste BD seja 50M P a .
Cada uma das hastes de ligação AB e CD tem uma seção transversal retangular uniforme de 6,3 × 25,4m m e está ligada à barra horizontal BCE por pinos de diâmetro igual a 25,4m m . Considerando que a te
Cada uma das quatro hastes verticais, ligadas às duas barras horizontais, tem uma seção transversal uniforme de 10 × 40m m e os pinos tem diâmetro de 14 mm. Determine o máximo valor da tensão normal m