Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 10
Sabendo-se que a haste de ligação BD tem uma seção transversal uniforme, de área igual a , determine a intensidade da carga para que a tensão normal na haste BD seja .
Passo 1
Neste problema temos de fazer duas coisa fundamentais:
- Achar a força interna atuante na haste BD.
- Determinar a força , que é o que o problema pede, por meio dos princípios da estática (somatório das forças e momentos serem zero).
Passo 2
Como o problema nos fornece a tensão da haste BD, , e a área, , então é só substituir na equação da tensão normal:
Passo 3
Agora vem a parte de estática para determinar . Para isso a gente tem que colocar as forças de reação nos pinos e .
Nós já calculamos e sabemos que vale . Mas observa que as forças foram colocadas decompostas em uma força vertical e outra força horizontal . Então a gente tem que achar essas duas forças por meio do ângulo .
Pela figura podemos ver que:
Podemos achar o tamanho da barra BD por meio do teorema de Pitágoras:
Logo,
Passo 4
Agora vamos achar , aplicando o momento em :
Nós não temos a altura mas podemos achar porque o ângulo de foi fornecido, assim:
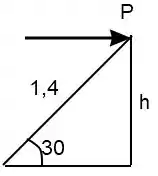
Pela geometria vamos ter que
Voltando ao cálculo do momento: