Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 72

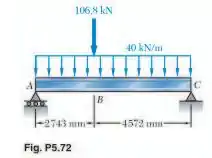
Sabendo que a tensão admissível para ao aço é de selecione a viga de mesa larga mais econômica para suportar o carregamento mostrado.

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Partiu mais questão.

Primeiramente, sabemos que a tensão normal é dada por:

Onde é o momento atuante na seção e é a propriedade da seção. Neste caso, vamos determinar o e depois escolher a seção que melhor se adequa no ábaco no fim do livro. A viga mais econômica será a de menor pois ela tem a menor seção e gastaria menos material.

Para determinar o momento, vamos traçar o diagrama e pegar o máximo valor do módulo do momento, que causa maior tensão na viga. Para isso, vamos determinar as reações. Aplicando as equações de equilíbrio:

Passo 2

Agora, basta traçar o diagrama de momento:

Podemos ver que o momento máximo é Logo:

Logo, substituindo:

Usando o ábaco, podemos ver que a seção mais econômica viável será:

Pronto, mais uma questão feita!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga A B suporta uma força uniformemente distribuída de 2k N / m e duas forças concentradas P e Q . Foi determinado experimentalmente que a tensão normal provocada pelo momento fletor na borda infer

Sabendo que a tensão admissível para ao aço é de 160M P a , selecione a viga de mesa larga mais econômica para suportar o carregamento mostrado.

Trace os diagramas de cortante e momento fletor para a viga e o carregamento mostrado, e determine a tensão normal máxima provocada pelo momento fletor.

Para a viga e o carregamento mostrados na figura, projete a seção transversal da viga sabendo que o tipo de madeira utilizada tem uma tensão normal admissível de 12M P a .

A viga A B suporta duas forças concentradas P e Q . A tensão normal provocada pelo momento fletor na borda inferior da viga é de + 55M P a em D e de + 37,5M P a em F . (a) Trace os diagramas de força