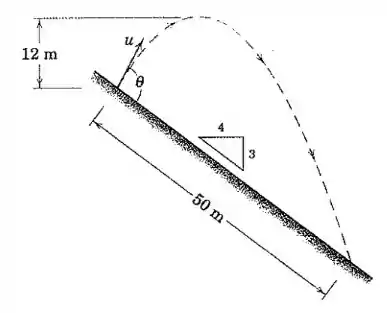
Uma pedra é lançada para baixo de uma encosta como mostrado. Determine o módulo e a direção da sua velocidade inicial de modo que a pedra suba e ainda tenha um alcance de metros para baixo da encosta.

Agora vamos procurar uma expressão para o alcance. Vamos aproveitar que já temos a componente vertical para ver o tempo que o nosso trajeto dura.

Usando a proporção do triângulo (conforme indicado na figura), a gente pode deduzir que a altura da encosta e a largura valem:

O movimento acaba quando a pedra bate no chão certo? Em outras palavras, se chamarmos a altura de onde a pedra é jogada de , a altura quando ela bate no chão é , então:

E substituindo os valores achamos o seguinte:

E agora a gente pode resolver essa equação quadrática para saber o tempo do movimento:

E excluindo a solução negativa ficamos com:

Então beleza, nosso movimento necessariamente vai demorar , se a gente quer que ele percorra os na horizontal nesse tempo, qual tem que ser a componente horizontal da velocidade inicial?

Lembre-se de que nesse caso não existe aceleração na direção horizontal.

Ótimo, agora já podemos calcular o módulo da velocidade :

E agora, como achar o ângulo ?

Muito cuidado aqui pessoal, não podemos dizer que , porque , nesse caso, não é o ângulo que o vetor faz com o eixo horizontal.

Precisamos fazer uma separação aqui:

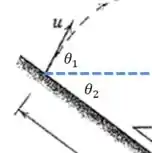
Agora perceba que o sim é o ângulo que faz com o eixo horizontal, ou seja:

E o ? Bom, olhando para a figura, é só fazer um pouco de geometria plana pra ver que ele é igual ao ângulo que a encosta faz com a horizontal, ou seja:

E agora é só lembrar que:

Pronto!