Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 111
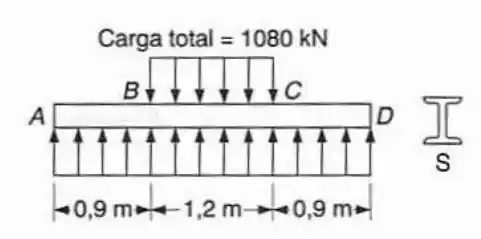
Sabendo-se que e , selecionar o perfil laminado para a viga, que poder ser usado para suportar o carregamento distribuído dado, quando este é colocado sobre o solo.
Passo 1
Oi, fala aí, galerinha!!! Para resolver esse problema a gente vai seguir o seguinte passo a passo:
- Calcular a força cortante, o momento fletor e achar o momento fletor máximo.
- Calcular o módulo resistente da seção .
- O item anterior nos fornecerá com um mínimo para que a viga resista às cargas. Logo, para achar o perfil temos de ir na tabela de perfis no final do livro e selecionar aqueles em que e seja o mais econômico.
Então partiu pro exercício!
Passo 2
Neste caso, como a viga esta apoiada no chão então não há forças de reação locais e sim uma força distribuída sobre toda a sua extensão. Podemos calcular essa forma da forma:
Para saber o valor da carga por unidade de distância:
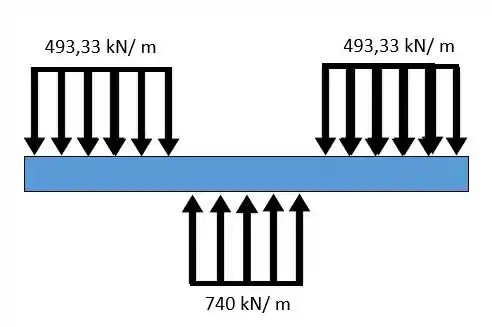
E podemos dividir também a carga total em um carregamento:
Assim podemos desenhar um novo carregamento, que considera apenas o resultado líquido:
Passo 3
Nós queremos o máximo momento fletor máximo e a força cortante máxima. Como estamos diante de um problema simétrico, então vamos ter que o momento fletor máximo será localizado na metade da barra () e neste ponto o cortante é zero, assim:
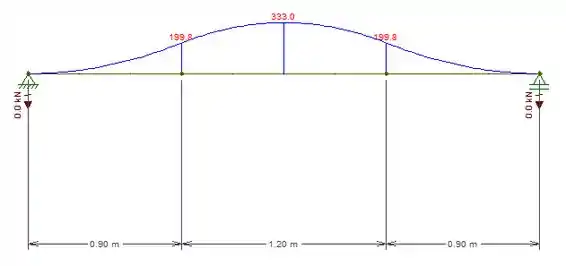
E a força cortante máxima ocorre nos pontos e :
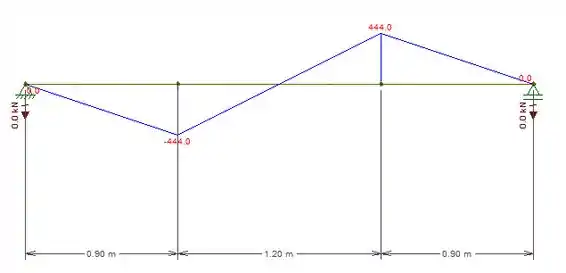
Passo 4
Agora vamos achar o momento resistente mínimo que a viga deve possuir , que é dado por:
Passo 5
Agora vamos para a nossa tabela e vamos escolher a viga com e a mais econômica. Aqui econômica significa a viga com a menor altura nominal, logo a nossa selecionada é a seção: