Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 130
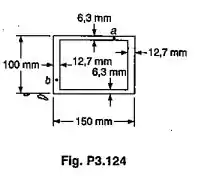
Sabendo-se que o eixo do Prob 3.124 tem 1,2m e que G=26 GPa, determinar o ângulo de torção causado pelo torque de
Passo 1
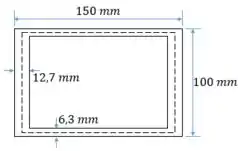
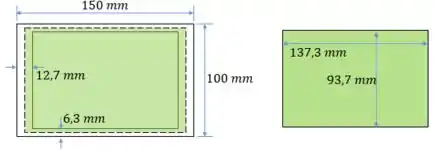
A melhor forma de começar questões de parede finas é calculando a área interna. Abaixo tem um desenho, onde já descontamos a espessura das paredes finas
Passo 2
Vamos calcular o ângulo de torção:
Calcular um integral de linha não é fácil. Mas por sorte, podemos evitar esse problema!
Uma integral de linha representa o contorno de uma região. Mas também devemos levar em consideração que a espessura varia.
Mas não tem problema, podemos fazer uma aproximação, calculando a integral por partes, da seguinte forma:
Passo 3
E agora é só calcular o ângulo de torção:
O ângulo de torção é:
Resposta
Exercícios de Livros Relacionados
Uma placa anular de espessura τ e módulo de elasticidade transversal G é utilizada para conectar o eixo AB de raio r 1 ao tubo CD de raio interno r 2 . . Sabendo que é aplicado um torque T á extremida
Dois eixos de seção transversal cheia, feitos de aço G = 77 , 2G P a , são conectados a um disco de acoplamento B e engastados ao suporte rígido em A e C. Para o carregamento mostrado, determine (a) a
(a) Para o eixo de aço com seção transversal cheia mostrado G = 77G P a , determine o ângulo de torção em A. (b) Resolva a parte (a) considerando que o eixo de aço é vazado com 30 mm de diâmetro exter
Determine o ângulo pelo qual a extremidade A gira quando T = 565N ⋅ mm, l = 61 mm, d = 1,59 mm, G=77,2 GPa e n=2 .
Dois eixos, cada um com diâmetros de22 , 2m m , são conectados pelas engrenagens mostradas na figura. Sabendo que G=77 , 2G P a e que o eixo está fixo em F , determine o ângulo pelo qual a extremidade