Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 94

Sabendo-se que o tubo estrutural mostrado tem uma espessura da parede uniforme de 6   m m , determinar a tensão de cisalhamento em cada um dos três pontos indicados.

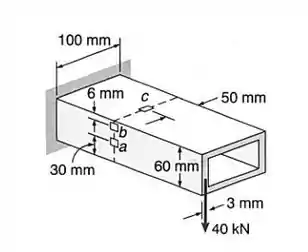
Passo 1

Fala aí galera, bora garantir aquele notão em Resmat? Para isso temos que resolver mais questões. Primeiro, vamos calcular o efeito cortante na direção da força que é aplicada no tubo (chamaremos de eixo y ), temos:

V y = - 40000   N

Agora, precisamos encontrar a posição da linha neutra, mostrada na figura:

y i = y s = 30   m m

Em seguida, para podermos calcular a tensão de cisalhamento, precisamos encontrar primeiro o momento de inércia da área da seção. Neste caso, dado por:

I z = b h 3 12 I z = 100 ∙ 60 3 12 - 88 ∙ 48 3 12 I z = 988992 × 10 - 12   m 4

Passo 2

Com isso, vamos encontrar o momento torsor, temos:

T = 40000 × 0,047 T = 1880   N ∙ m

Logo, a tensão de cisalhamento por momento torsor vai ser:

τ T = T 2 t ∙ A m = 1880 2 0,006 × 0,094 × 0,054 τ T = 30864197,53   P a

Passo 3

Com os dados obtidos, podemos calcular a tensão de cisalhamento para cada ponto pedido. Esta vai ser obtida através da soma da tensão de cisalhamento por força cortante e da tensão de cisalhamento pelo momento torsor. Fica assim:

τ n = τ V y + τ T

Para o ponto a , temos:

τ a = τ V y + τ T

E então, vamos encontrar tensão de cisalhamento por força cortante, dada por:

τ V y = V Q I ∙ b

Onde:

b = 0,006 × 2 = 0,012   m

Para encontrarmos o momento estático, precisamos encontrar a distância do centro de gravidade da área até o eixo. Temos:

Q = A ' ∙ y ' -

y ' - = 2 0,006 0,030 0,015 + 0,088 0,006 0,027 2 0,006 0,030 + 0,088 0,006 y ' - = 0,022135135   m

Substituindo:

Q = 2 0,006 0,030 + 0,088 0,006 0,022135135 Q = 19,65599988 × 10 - 6   m 3

Assim, podemos encontrar a tensão de cisalhamento no ponto a . Temos:

τ a = - 40000 19,65599988 × 10 - 6 988992 × 10 - 12 0,012 + 30864   197,53 τ a = 97,11   M P a

Passo 4

Para o ponto b , basta repetirmos o processo. Fica assim:

τ b = τ V y + τ T

Onde:

b = 0,006 × 2 b = 0,012   m

Nosso momento estático vai ser:

Q = A ' ∙ y ' - y ' - = 0,027   m

Q = 0,1 ∙ 0,006 0,027 Q = 16,2 × 10 - 6   m 3

Com isso, temos que τ b vai ser dado por:

τ b = - 40000 16,2 × 10 - 6 988992 × 10 - 12 0,012 + 30864   197,53 τ b = 85,47   M P a

Passo 5

Por último, para c , o processo vai ser menos complicado pois o nosso momento estático vai ser zero, pois o ponto c já está na beirada. Logo, a tensão de cisalhamento vai ser:

τ c = τ V y + τ T τ c = 0 + τ T τ c = 30,86   M P a

Resposta

τ a = 97,1   M P a

τ b = 85,5   M P a

τ c = 30,9   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.
Dormentes de ferrovia devem ser projetados para resistir a grandes carregamentos de cisalhamento. Se o dormente for submetido a cargas de 150 kN exeridas pelos trilhos e o leito de cascalho exercer um
Desenvolva uma expressão para a componente vertical média da tensão de cisalhamento que age no plano horizontal que passa pelo eixo, localizado a uma distância y do eixo neutro.
Se a força P=4kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.
Determine as maiores forças P que o elemento pode suportar se a tensão de cisalhamento admissível for τ a d m = 70M P a . Os apoios em A e B exercem somente reações verticais sobre a viga.