Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 16

A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.

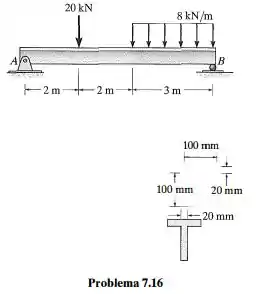
Passo 1

A questão pede que determinemos a tensão máxima. Vamos começar determinando as reações de apoio.

∑ M B = 0 ⇒ R A ⋅ 7   m - 20   k N ⋅ 5   m - 8 k N m ⋅ 3   m ⋅ 1,5   m = 0

R A = 19,43   k N

∑ F y = 0 ⇒ R A - 20   k N - 8 k N m ⋅ 3   m + R B = 0

R B = 24,57   k N

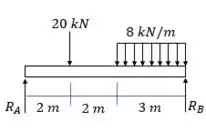
Passo 2

Agora utilizamos o método gráfico para gerar um diagrma de esforço cortante

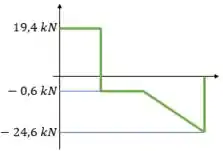
Pelo gráfico observamos que o esforço máximo interno na viga é:

V m a x = - 24,6   k N

Passo 3

Agora vamos observar a seção transversal. Começamos com o centroide

y c = 20 ⋅ 100 ⋅ 50 + 100 ⋅ 20 ⋅ 110 20 ⋅ 100 + 100 ⋅ 20

y c = 80   m m

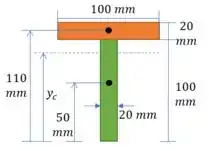
Passo 4

E agora calculamos o momento de inércia:

I = I v e r d e + I l a r a n j a

I = 20 ⋅ 100 3 12 + 20 ⋅ 100 ⋅ 30 2 + 100 ⋅ 20 3 12 + 100 ⋅ 20 ⋅ 30 2

I = 5,33 ⋅ 10 6   m m 4

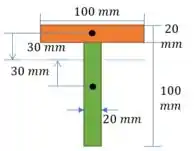
Passo 5

Vamos calcular o Momento Estático máximo. Por facilidade, vamos escolher a região inferior:

Q = A v e r d e ⋅ y v e r d e

Q = 20 ⋅ 80 ⋅ 40

Q = 64000   m m 3

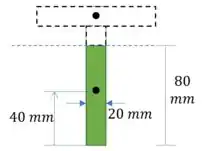
Passo 6

E agora é só aplicar a equação 7.3:

τ = V Q I t

Substituíndo os valores:

τ = 24,6   k N ⋅ 64000   m m 3 5,33 ⋅ 10 6   m m 4 ⋅ 20   m m

τ = 14 , 77   M P a

Resposta

τ = 14,77   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três pranchas de 50 x 100 mm são pregadas juntas para formar um viga que é submetida a uma força cortante de 1500 N. Sabendo que a tensão de cisalhamento admissível em cada prego é de 400 N, determine
Uma viga caixão quadrada é feita de duas pranchas 20 x 80 mm e duas pranchas de 20 x 120 mm pregadas entre si, como mostrado na figura. Sabendo que o espaçamento entre os pregos é de s= 30 mm e que a
Para a viga e carregamento mostrado, considere a seção n-n e determinar (a) o maior tensão de cisalhamento nessa seção, (b) a tensão de cisalhamento ponto a.
A viga de seção composta mostrada foi fabricada conectando dois perfis laminados W150x29,8 por meio de parafusos com 15,88m m ,Sabendo que a tensão de cisalhamento média admissível para os parafusos é
Para a viga e carregamento mostrado, considere a seção n-n e determinar (a) o maior tensão de cisalhamento nessa seção, (b) a tensão de cisalhamento ponto a.