Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 73a
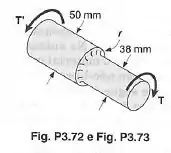
Sabendo-se que a tensão de cisalhamento admissível é de para o eixo escalonado mostrado, determinar a intensidade do maior torque que pode ser transmitido pelo eixo, quando o raio de adoçamento é: (a)
Passo 1
Temos um eixo escalonado. Nesse caso, as tensões máximas ocorrem onde há concentração de tensões, ou seja, onde há mudança de seção. E para descobrir essas tensões a gente usa a fórmulinha:
Mas agora a gente tem a tensão máxima e quer o torque máximo que pode haver. Então usamos:
Nossos dados são:
- Diâmetro maior:
- Diâmetro menor: , logo o raio menor é:
- Raio do adoçamento:
- Tensão máxima:
Vem comigo!
Passo 2
Para um eixo maciço, temos que:
Substituindo isso na fórmulinha de tensões concentradas:
Passo 3
Temos todos os dados, menos o . A gente acha ele pelo gráfico:
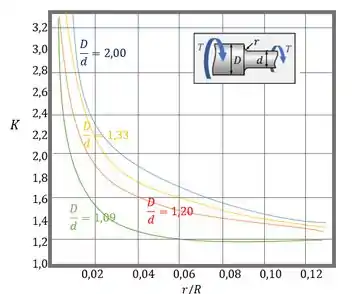
Vamos achar primeiro a relação , para ver qual curva usar:
Então, a gente usa a curva onde , que é a amarelinha. Agora a gente acha :
O ponto na curva de nos leva ao valor de .
Passo 4
Já que temos tudo, vamos substituir na fórmulinha: