Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 169

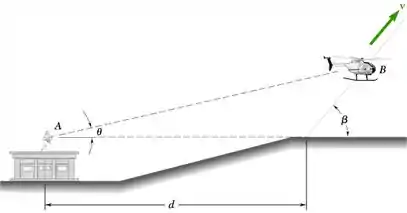
Após a decolagem, um helicóptero sobe em linha reta em um ângulo constante de rampa β . Seu voo e rastreado por um radar localizado no ponto A. Determine a velocidade escalar do helicóptero em termos de d, β ,   θ e θ ˙ .

Passo 1

E ai galera partiu determinar a velocidade escalar do helicóptero em termos de d, β ,   θ e θ ˙ . Vamos fazer um esboço para facilitar nossa vida :D

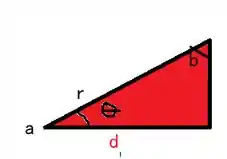
Do diagrama

r sin ⁡ 180 ° - β = d sin ⁡ β - θ

ou

d sin ⁡ β = r sin ⁡ β cos ⁡ θ - cos ⁡ β sin ⁡ θ

ou

ou

r = d tan ⁡ β tan ⁡ β cos ⁡ θ - sin ⁡ θ

Então

r ˙ = d tan ⁡ b - - tan ⁡ β sin ⁡ θ - cos ⁡ θ tan ⁡ β cos ⁡ θ = d θ tan ⁡ β tan ⁡ β sin ⁡ θ + cos ⁡ θ ( tan ⁡ β cos ⁡ θ - sin ⁡ θ ) 2

Do diagrama

v r = v cos ⁡ β - θ             onde             v r = r ˙

Então

d θ ˙ tan ⁡ β tan ⁡ β sin ⁡ θ + cos ⁡ θ ( tan ⁡ β cos ⁡ θ - sin ⁡ θ ) 2 = v cos ⁡ β cos ⁡ θ + sin ⁡ β sin ⁡ θ

= v cos ⁡ β tan ⁡ β sin ⁡ θ + cos ⁡ θ

Passo 2

Solução alternativa.

Nós temos

v 2 = v r 2 + v θ 2 = ( r ˙ ) 2 + ( r θ ˙ ) 2

Usando as expressões para r e r ˙ acima

v = d θ ˙ tan ⁡ β tan ⁡ β sin ⁡ θ + cos ⁡ θ ( tan ⁡ β cos ⁡ θ - sin ⁡ θ ) 2 2

ou

v = ± d θ ˙ tan ⁡ β tan ⁡ β cos ⁡ θ - sin ⁡ θ ( tan ⁡ β sin ⁡ θ + cos ⁡ θ ) 2 ( tan ⁡ β cos ⁡ θ - sin ⁡ θ ) 2 + 1 1 / 2 = ± d θ ˙ tan ⁡ β tan ⁡ β cos ⁡ θ - sin ⁡ θ tan 2   β + 1 ( tan ⁡ β cos ⁡ θ - sin ⁡ θ ) 2 1 / 2

Observe que à medida que o aumenta, o helicóptero se move na direção indicada. Assim, a raiz positiva é escolhida.

Resposta

v = d θ ˙ tan ⁡ β sec ⁡ β ( tan ⁡ β cos ⁡ θ - sin ⁡ θ ) 2

v = d θ ˙ tan ⁡ β sec ⁡ β ( tan ⁡ β cos ⁡ θ - sin ⁡ θ ) 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a bola de beisebol do Prob. 2/51 atirada para cima com uma velocidade inicial de 30m / s , determine o tempo t s do solo até o ápice e o tempo t d do ápice até o solo.Prob. 2/51: Quando o efeito
Quando o efeito de arrasto aerodinâmico é incluído, a aceleração y de uma bola de beisebol movendo-se verticalmente para cima é a u = - g - k v 2 , enquanto a aceleração quando a bola está movimento d
Os pavimentos de um edifício alto são uniformemente espaçados de 3 metros de altura. Uma bola A é deixada cair da posição mostrada do telhado. Determine os tempos necessários para que esta passe os 3
Um trem é composto de uma locomotiva com 180t e cem vagões com 90t . Se a locomotiva exerce uma força de atrito de 180k N sobre os trilhos na partida do trem a partir do repouso, calcule as forças nos
A talha é liberada a partir do repouso com todos os cabos esticados. Despreze o atrito e a massa de todas as polias e determine a aceleração de cada cilindro e as trações T 1 e T 2 nos dois cabos.