Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 8
3.8. Sabe-se que uma força vertical de é necessária para remover da tábua o prego fixado em C. Ao primeiro movimento do prego, determine (a) o momento em relação a B da força exercida sobre o prego, (b) a intensidade da força P que cria o mesmo momento em relação a B se , (c) a menor força P que cria o mesmo momento em relação a B.
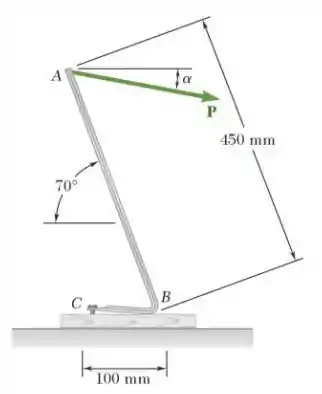
Passo 1
Bem, quase todo exercício de mecânica fica mais simples resolver se fizermos um desenho da situação destacando o que a gente precisa.
Passo 2
O momento de uma força é definido por
Onde
Momento
Força
distância
Então
Vamos colocar a distância no SI
E essa é a resposta do item (a)
Passo 3
Agora para fazer o item (b) vamos usar
Bem como estamos definindo o momento em relação à B e a força está sendo aplicada em A, a força paralela ao vetor não faz nenhuma diferença para o calculo do momento. Então vamos usar só , que olhando pela imagem temos
Mas falta determinar quem é , repare que
Então
Para determinar a intensidade de usamos
Mas essa distância agora é a distância perpendicular à entre A e B, logo
Então
E essa é a resposta do item (b)
Passo 4
Agora só falta o item (c)
Bom uma das propriedades do produto vetorial é que seu valor vai ser máximo se os dois vetores forem perpendiculares, em outras palavras a Força tem que ser perpendicular ao vetor distância A e B.
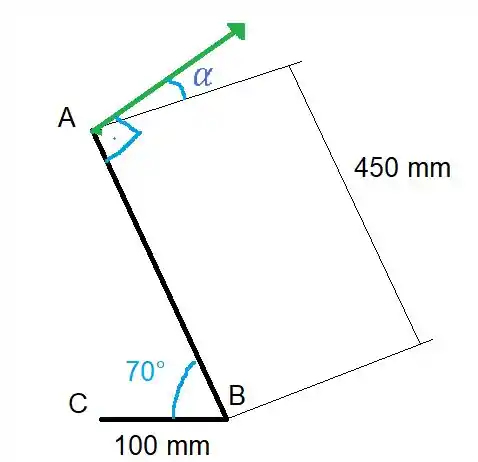
Então podemos fazer
Resposta
Item (a)
Item (b)
Item (c)