Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 21
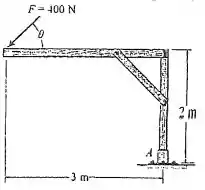
Determine a direção da força de modo que ela produza o momento máximo em relação ao ponto . Calcule esse momento.
Passo 1
Oi, galerinha! Tudo bom? Pra começar vamos pensar em alguns conceitos sobre o momento de uma força.
Lembra que o vetor momento é dado por:
Como isso é um produto vetorial, podemos escrever na forma escalar como:
Onde é o ângulo entre os vetores força e distância. E visto que o momento depende então da função seno, ela terá o seu valor máximo quando:
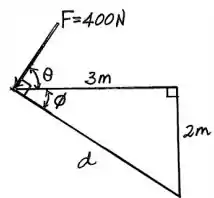
Ou seja, o momento máximo desejado ocorrerá quando a força estiver sendo aplicada perpendicularmente à linha que liga o ponto de atuação da força até o ponto como mostrado no desenho a seguir:
Passo 2
Dessa forma, deve-se determinar o ângulo no qual a força estará incidindo no corpo:
Como o ângulo é complementar de , tem-se que:
Passo 3
Sendo assim, suponde que o momento seja positivo no sentido anti-horário, o momento máximo gerado em poderá ser calculado diretamente através da distância :
Ou poderá ser determinado através das componentes da força aplicada e do princípio dos momentos: