Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 11
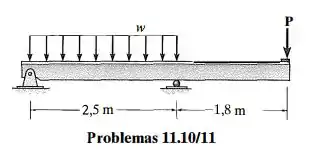
Selecione no Apêndice B a viga de aço de abas largas de menor peso e altura que suportará com segurança as cargas mostradas na figura, na qual e . A tensão de flexão admissível é e a tensão de cisalhamento admissível é
Passo 1
Fala, meu querido! Essa é uma questão de projetar dimensões e escolher uma seção para essa viga. Então a gente precisa achar as piores situações a que a essa viga está submetida. Para isso, precisamos descobrir os esforços de cortante e momento máximo.
Dados da questão:
A questão pede: O tipo de viga.
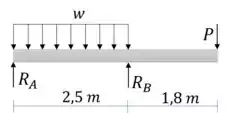
Passo 2
Começamos com as reações de apoio.
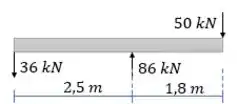
Passo 3
Utilizando o método gráfico e a tabela 6.1 geramos os diagramas de esforço cortante e momento fletor. Vamos usar o método gráfico porque só temos forças concentradas. Aí fica mais simples.
O gráfico de esforço cortante é gerado diretamente utilizando a tabela, basta subtrair ou adicionar o valor das forças a medida em que o gráfico passa por elas.
Como , descemos esse valor (seguindo o sentido da força), ficamos constante até a próxima força de . Seguimos o sentido dela, e subimos , depois ficamos constante até , e descemos esse valor, seguindo o sentido da força.
Como chegamos no zero, nossa conta está certinha.
Utilizando as áreas abaixo do gráfico de esforço cortante podemos gerar o gráfico de momento fletor. O momento em um ponto vai ser a soma algébrica das áreas que aparecem antes do ponto em questão.
Como nossa viga só tem cargas concentradas, a gente só precisa ligar esses pontos por retas.
Fica assim:
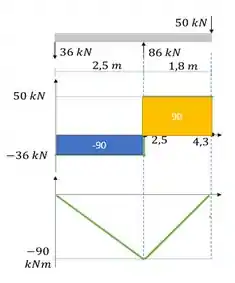
Assim encontramos os esforços máximos na viga:
Passo 4
Agora vamos achar . Um critério para gente escolher a viga que vai aguentar com segurança o momento máximo. Pelo qual podemos escolher a seção da viga na tabelinha do apêndice .
Aplicamos a equação 11.1 para determinar esse :
Passo 5
Agora gente procura no apêndice B uma viga com a seção que tenha um um pouco maior que esse. Repara lá que tem em relação ao eixo e ao . Aí a gente pensa: em torno de que eixo nossa seção sofre o momento? Em torno do . Então a gente vê nessa coluna.
Escolhendo a viga de aço de abas largas de menor peso e altura, temos
Com as seguintes propriedades:
Passo 6
Como esta é uma viga de abas largas, podemos utilizar a equação a seguir para estimar a tensão de cisalhamento máximo do nosso carregamento:
Como a tensão de cisalhamento admissível é de a viga selecionada é compatível com o projeto