Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 13
Selecione no Apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é e a tensão de cisalhamento admissível é
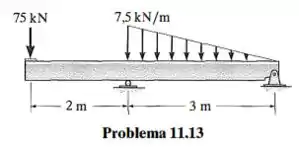
Passo 1
E aí? Vamos lá? A ideia aqui é usar os critérios de projeto para escolher essa viga. E aí gente vai dimensionar ela com base nas situações extremas. Por isso, a gente precisa descobrir o valor das tensões máximas, ok?
Para fazer isso é só seguir esse passo a passo que vamos fazer. Bora lá!
Primeiro calculamos a força equivalente ao carregamento distribuído:
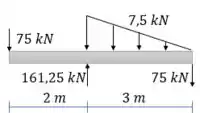
E calculamos as reações de apoio
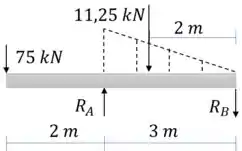
Passo 2
Vamos utilizar a Tabela 6.1 do livro pra gerar os diagramas de momento fletor e esforço cortante:
E como a gente usa essa tabela? Do lado esquerdo da viga a gente imagina que temos uma viga engastada. E no lado direto, onde tem o carregamento distribuído, a gente imagina que temos uma viga biapoiada com carregamento triangular.
Aí o diagrama fica assim:
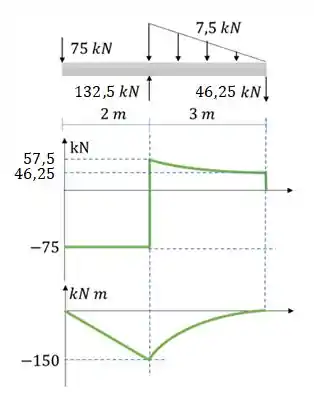
E achamos os valores máximos:
Passo 3
Vamos verificar a resistência sobre flexão pela equação 11.1, o critério :
Pelo apêndice B selecionamos a viga
Passo 4
Agora vamos testar se nossa viga resiste ao cisalhamento. Como é uma viga de abas largas podemos utilizar:
A tensão que é gerada na viga é:
A tensão admissível é de , o que garante que a viga selecionada resiste ao esforço.