Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 4
Selecione no Apêndice B a viga de aço de abas largas de menor peso que suportará com segurança a carga da máquina mostrada na figura. A tensão de flexão admissível é e a tensão de cisalhamento admissível é .
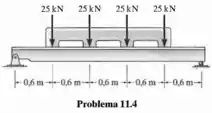
Passo 1
Começamos com as reações de apoio.
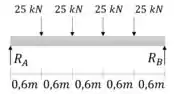
Como o carregamento é simétrico:
Pelas equações de equilíbrio:
Passo 2
Pelo método gráfico podemos gerar o diagrama de esforço cortante e momento fletor
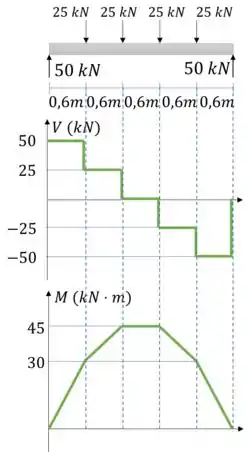
Passo 3
Vamos verificar a resistência da viga em relação ao momento e a tensão normal
Aplicando os valores:
Observando o apêndice selecionamos:
As propriedades dessa viga são:
Passo 4
Vamos verificar a resistência contra o cisalhamento
Aplicando:
Como é menor que a tensão admissível , isso garante que a viga selecionada é apropriada
Resposta
Exercícios de Livros Relacionados
As vigas do assoalho de um galpão de depósito devem ser selecionadas em função de vigas quadradas de madeira feitas de carvalho. Se cada viga tiver de ser projetada para suportar uma carga de 7,5k N /
Resolva o Problema 11.6 se a seção transversal tiver largura desconhecida, mas tiver de ser quadrada, isto é,h = b
A viga de madeira de ser carregada como mostra a figura. Se as extremidades suportarem somente forças verticais, determine o maior valor de P que pode ser aplicado. σ a d m = 25 M P a ,τ a d m = 700k
A viga de madeira tem seção transversal retangular e é usada para suportar uma carga de 6 kN. Se a tensão de flexão admissível for σ = 14M P a , τ = 5M P a , determine a altura h da seção transversal