Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 7

Resolva o Problema 11.6 se a seção transversal tiver largura desconhecida, mas tiver de ser quadrada, isto é,   h = b

Passo 1

Começamos calculando as reações de apoio

∑ M B = 0 ⇒ R A ⋅ 3 - 6 ⋅ 1,8 = 0

R A = 3,6   k N

∑ F Y = 0 ⇒ R A - 6 + R B = 0

R B = 2,4   k N

Passo 2

Pelo método gráfico geramos um diagrama de momento fletor e esforço cortante:

V m a x = 3,6   k N

M m a x = 4,32   k N ⋅ m

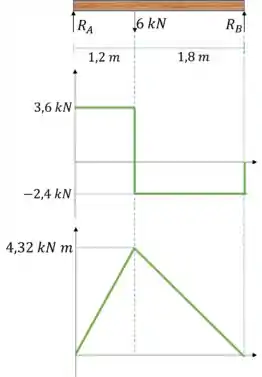
Passo 3

Aplicando a equação do momento fletor:

σ m a x = M m a x S

S = M m a x σ m a x

Lembrando que S = I / c

I c = M m a x σ m a x

1 12 h 4 h / 2 = M m a x σ m a x

h 3 6 = M m a x σ m a x

Isolando h :

h 3 = 6 ⋅ M m a x σ m a x

h 3 = 6 ⋅ 4,32   k N   m 14   M P a

h = 122,8   m m

Com precisão de 5 mm:

h = 125   m m

Passo 4

Vamos analisar a tensão de cisalhamento. Como a viga é retangular maciça a fórmula é

τ = 1,5   V A

Substituindo os valores:

τ = 1,5   V h 2

Isolando b

h 2 = 1,5   V τ

Aplicando os valores

h 2 = 1,5 ⋅ 3,6   k N 5   M P a

h = 32,86   m m

Com precisão de 5 mm

h = 35   m m

Passo 5

Para garantir a resistência, escolhemos a maior dimensão:

h = 125   m m

Resposta

h = 125   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Selecione no Apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é σ a d m = 168M P a e a tensão de cisalhame
Determine, com aproximação de múltiplos de 5 mm, a largura mínima da viga que suportará com segurança a carga P = 40 k N . A tensão de flexão admissível é σ a d m = 168M P a e a tensão de cisalhamento
Selecione no Apêndice B a viga de aço de abas largas de menor peso e altura que suportará com segurança as cargas mostradas na figura, na qual w = 0 e P = 50k N . A tensão de flexão admissível é σ a d
Trace os diagramas de força cortante e momento fletor para a viga W310x21 e verifique se ela suportará com segurança a carga mostrada na figura. A tensão de flexão admissível é σ a d m = 160M P a e a
A viga simplesmente apoiada é composta por duas seções W310x33 montadas como mostra a figura. Determine a carga uniforme máxima w que ela suportará se a tensão de flexão admissível for σ a d m = 160M