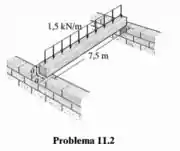
As vigas do assoalho de um galpão de depósito devem ser selecionadas em função de vigas quadradas de madeira feitas de carvalho. Se cada viga tiver de ser projetada para suportar uma carga de sobre um vão simplesmente apoiado de 7,5 m, determine a dimensão a de sua seção transversal quadrada com aproximação de múltiplos de 5 mm. A tensão de flexão admissível é e a tensão de cisalhamento admissível é

Utilizamos o método gráfico para gerar os diagramas de esforço cortante e momento fletor.

Vamos calcular as propriedades geométricas da seção!

O momento de inércia é:

Ponto de maior tensão normal:

Momento estático:

Vamos calcular o tamanho que a seção precisa ter pra resistir ao momento:

Aplicamos agora a equação 6.11 da tensão normal máxima:

Aplicando os valores:

Isolando o

A seção é:

Arredondando com precisão de 5 mm:

Vamos calcular o tamanho que a seção precisa ter pra resistir ao cisalhamento:

Aplicamos a equação do cisalhamento:

Isolando o

A seção mínima para resistir ao cisalhamento é:

Arredondando com precisão de 5 mm:

Para garantir a resistência, devemos selecionar o maior valor de