Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 3
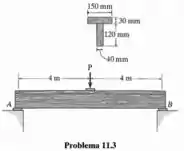
A viga de madeira de ser carregada como mostra a figura. Se as extremidades suportarem somente forças verticais, determine o maior valor de P que pode ser aplicado.
Passo 1
Fala! A gente quer o maior valor de , certo? Basicamente, o que a gente pode fazer é achar as tensões máximas nessa viga em função de e comparar com a tensões admissíveis. Aí o menor valor de que a gente achar vai ser nossa resposta.
Queremos as tensões máximas, então precisamos pelas reações de apoio.
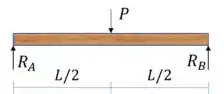
Como a carga é simétrica:
Pelas equações de equilíbrio:
Passo 2
Queremos achar os esforços máximos. Vamos fazer os diagramas.
Para o diagrama do cortante podemos usar “a jornada do cortante”. Para esse caso, ela funciona assim: como no começo a gente tem uma carga para cima, nós subimos esse valor e depois ficamos constantes até a carga pontual .
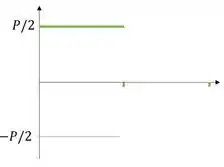
Depois, como essa carga está para baixo, a gente desce esse valor e depois continua constante até a próxima carga . E aí como essa carga está para cima, a gente sobe esse valor e fecha nosso diagrama:
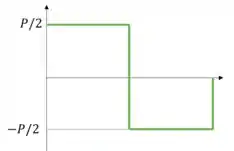
Vemos que o cortante máximo é:
Para o momento, podemos lembrar que para uma viga biapoiada com carga no meio, o momento máximo é no meio. Então a gente calcula o momento nessa seção.
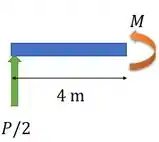
Passo 3
Vamos calcular as propriedades geométricas da seção!
O centroide da seção é:
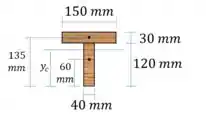
O momento de inércia é:
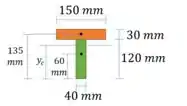
Ponto de maior tensão normal:
Momento estático:
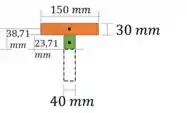
Repara que a gente calculou o momento estático na linha que passa pelo centroide. Isso porque é nessa linha que ocorre o cisalhamento máximo.
Passo 4
Vamos calcular agora a tensão máxima normal causada pelo momento em função de e compara-lá a tensão normal admissível.
Aplicamos agora a equação 6.11 da tensão normal máxima:
Para essa tensão ser máxima, precisamos que seja o ponto mais distante do eixo que passa pelo centroide. Logo, .
Aplicando os valores:
Isolando o :
A força é:
Passo 5
Vamos calcular agora o cisalhamento máximo causado pelo cortante em função de e compara-lo a tensão de cisalhamento admissível.
Aplicamos a equação do cisalhamento:
Onde é a expessura da nossa seção na linha estudada, .
Isolando o
A força é:
Passo 6
Para garantir a resistência, devemos selecionar o menor valor de