Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 100
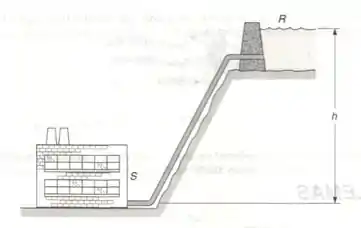
Uma tubulação de água de de diâmetro externo e de espessura da parede liga um reservatório com uma estação geradora . Sabendo-se que , determinar a máxima tensão normal e a máxima tensão de cisalhamento na tubulação, sob condições estáticas. [.]
Passo 1
Fala galerinha, essa questão pode parecer mais complexa ou mais difícil, mas pode ficar tranquilo porque o passo a passo é muito tranquilo, vamos nessa?
- Sabemos que a nossa tubulação é cilíndrica e não esférica, nesse caso, usaríamos as seguintes equações:
- Sabemos que o nosso diâmetro dado, é o diâmetro externo, ou seja, precisamos descontar a espessura, sendo assim temos que:
- E sabemos que é a espessura
- é a pressão que age na no ponto mais baixo da nossa tubulação, e sabemos que para calcular isso, precisamos usar a seguinte equação:
Com isso podemos fazer as nossas contas. Vamos lá?
Passo 2
Sabemos pelo enunciado que:
Calculando o raio, temos que:
Calculando a tensão, teremos que:
Assim temos que:
Resposta
Exercícios de Livros Relacionados
Resolver o Prob. 6.94, considerando que o sentido da força P é o inverso.
O estado de tensões mostrado irá ocorrer em um componente de alumínio fundido. Sabendo-se que para a liga de alumínio usada σ u t = 60MPae σ u c = 120MPa, e usando o critério de Mohr, determinar a ten
O estado de tensões mostrado irá ocorrer em um componente de alumínio fundido. Sabendo-se que para a liga de alumínio usada σ u t = 60MPae σ u c = 120MPa, e usando o critério de Mohr, determinar a ten
O estado plano de tensões indicado é esperado em um componente de ferro fundido. Sabendo-se que para a classe de ferro fundido usada σ u t = 170MPae σ u c = 340MPa, e usando o critério de Mohr, determ
O estado plano de tensões indicado é esperado em um componente de ferro fundido. Sabendo-se que para a classe de ferro fundido usada σ u t = 80MPae σ u c = 200MPa, e usando o critério de Mohr, determi