Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 175
Uma série de flutuadores esféricos são igualmente espaçados e firmemente presos a um cabo flexível de 20 m de comprimento. As extremidades A e B estão ancoradas a 16 m de distância, no fundo de um lago de água doce, a uma profundidade de 8 m. Os flutuadores e o cabo têm um peso combinado de 100 N por metro de comprimento do cabo, e a flutuabilidade da água produz uma força ascendente de 560 N por metro de comprimento do cabo. Calcule a profundidade h abaixo da superfície até o topo da linha de flutuadores. Encontre também o ângulo formado pela linha de flutuadores com a horizontal em A.
Passo 1
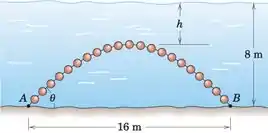
Primeiro, vamos desenhar o diagrama de corpo livre do cabo. Observe que a tensão TA machos ângulo com a horizontal e que substituímos os efeitos no cabo de peso e flutuabilidade por R resultante
Como o cabo tem uma forma de catenária de cabeça para baixo, invertemos o sistema de coordenadas de modo que a direção positiva do eixo y seja direcionada para baixo.
Neste sistema de coordenadas, o peso (w) tem efeito negativo, enquanto a flutuabilidade (wB) tem efeito positivo, então o efeito total no cabo por comprimento é:
Passo 2
Como o comprimento do cabo é s = 20 m, podemos calcular o R resultante
Também podemos ver pelo sketeh que a distância h é igual a:
Passo 3
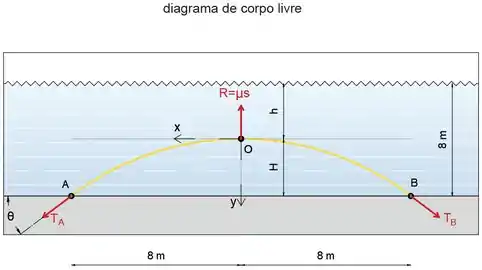
Observe que o comprimento do cabo do ponto O a A é igual à parada do comprimento total.
Também podemos escrever a expressão para o comprimento da parte OA como:
Substitua sA, e xA por seus valores de forma que a única incógnita na equação seja T0.
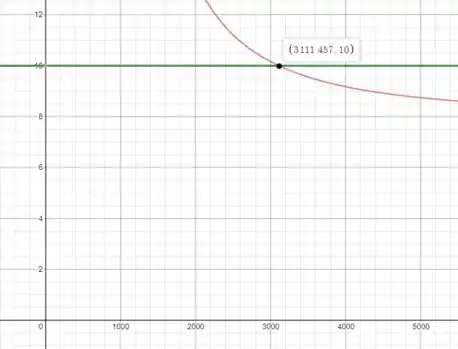
Usando uma calculadora gráfica como o Desmos (link nos comentários), plotaremos a função e leremos o valor de T0 em .
Passo 4
Usando a expressão (5/19) para função do cabo, podemos determinar o afundamento H.
Substitua T0 e por seus valores e coloque as coordenadas do ponto A na equação
Finalmente substitua H por seu valor na expressão (1) para determinar a distância h
Passo 5
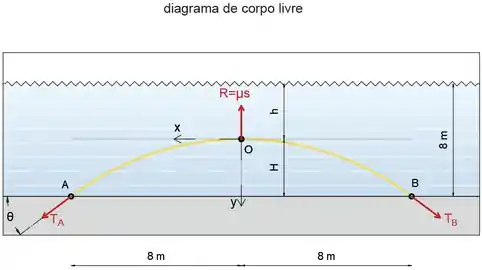
Agora, considere o diagrama de corpo livre da Etapa 1. (o diagrama também é carregado nesta etapa por conveniência)
Observe que as tensões em A e B são desconhecidas, mas podemos determiná-las usando a expressão (5/21)
Substitua , T0 e xA por seus valores.
Passo 6
Finalmente, ao igualar a soma dos momentos sobre o ponto B a zero, a única incógnita será o ângulo
A partir daqui, podemos expressar sin como:
Substitua R e TA por seus valores.
Finalmente, podemos expressar o ângulo como: