Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 181
Um comprimento de cabo com massa de 1,2 kg / m deve ter uma curvatura de 2,4 m quando suspenso dos dois pontos A e B na mesma linha horizontal de 10 m de distância. Para fins de comparação, determine o comprimento L de cabo necessário e plote sua configuração para os dois casos de (a) assumir uma forma parabólica e (b) usar o modelo catenário adequado. Para distinguir mais claramente entre os dois casos, plote também a diferença (yc yp) como uma função de x, onde C e P referem-se a catenária e parábola, respectivamente. Use a aproximação conforme declarado nas Eqs. (5/16) e (5 / 16a) conforme necessário.
Passo 1
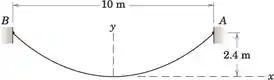
Para determinar o comprimento do cabo, vamos precisar das coordenadas do ponto A, peso do cabo por unidade de comprimento e o componente horizontal de tensão no cabo.
Pelo esboço, podemos ver que as coordenadas do cabo no ponto A são:
E que o peso do cabo é:
Enquanto a tensão T0 é desconhecida.
Passo 2
a) forma parabólica
Observe que a função do cabo parabólico é:
A partir daqui, podemos expressar T0 como:
Colocando as coordenadas do ponto A na equação e substituindo w por seu valor, podemos determinar o valor de T0
Finalmente, substitua T0 e w por seus valores na expressão (P) para obter a expressão de yp como função de x
Podemos determinar o comprimento do cabo diretamente usando a expressão (5 / 16a)
Passo 3
Onde L é a distância horizontal entre os pontos A e B, e h é a curvatura.
Observe que, desde , os primeiros três termos da equação para S fornecerão resultados precisos.
Substitua L e h na expressão de S
Passo 4
b) forma catenária
Como as coordenadas do ponto A são conhecidas, podemos escrever a expressão para o comprimento do cabo do ponto A até o início do sistema de coordenadas, ou seja, o comprimento da metade do cabo.
Podemos substituir e xA por seus valores e expressar SC como:
Passo 5
Observe que ainda há uma incógnita na equação acima (T0).
A função do cabo catenário é:
Colocando as coordenadas do ponto A, e substituindo pelo seu valor na expressão acima, teremos apenas uma incógnita atuando na equação (T0).
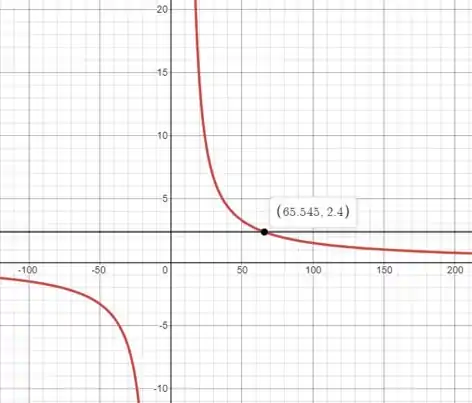
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos a função e seu valor de leitura em
Resultado lido no diagrama:
Passo 6
Colocando o valor de T0 na expressão (1), vamos calcular o comprimento do cabo
E ao colocar os valores de e T0 na expressão (C), escreveremos a expressão de yC como função de x
Finalmente, precisaremos escrever a expressão para a diferença entre yC e yP como função de x.
Substitua yC e yP por expressões (C*) e (P*)
Passo 7
Vamos organizar a expressão acima um pouco.
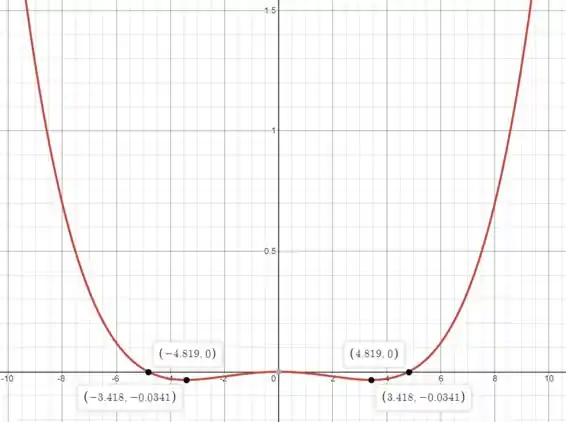
Finalmente, usando uma calculadora gráfica como o Desmos, vamos traçar a diferença d
Ao analisar o diagrama podemos concluir que a diferença é significativa para x > 5 m
Resposta
Ao analisar o diagrama, podemos concluir que a diferença é significativa para x > 5 m