Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 179

O cirurgião arbóreo tenta puxar para baixo o tronco da árvore parcialmente serrado. Ele cria uma tensão TA = 200 N na corda, que tem massa de 0,6 kg por metro de seu comprimento. Determine o ângulo θ A em que ele puxa, o comprimento L da corda entre os pontos A e B e a tensão TB no ponto B.

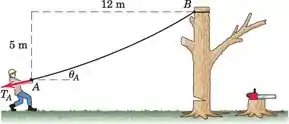
Passo 1

Nesta tarefa, precisamos determinar o ângulo 0, o comprimento da corda e a tensão no ponto B.

A tensão no ponto A é 200 N.

A corda tem massa de 0,6 kg por metro.

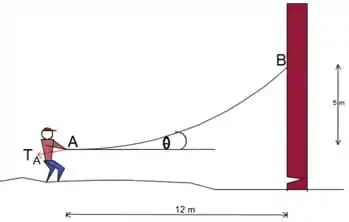
Usando a frase para determinar y, obteremos duas equações.

y = T 0 μ cosh ⁡ μ x T 0 - 1

y A = T 0 μ cosh ⁡ μ x A T 0 - 1

y A = T 0 5.89 cosh ⁡ 5.89 x A T 0 - 1

y B = T 0 μ cosh ⁡ μ x B T 0 - 1

y A + 5 = T 0 5.89 cosh ⁡ 5.89 x A + 12 T 0 - 1

T A = T 0 + μ y A

200 = T 0 + 5.89 × y A

T 0 = 200 - 5.89 × y A

Passo 2

Substituindo a equação T0 = 200 – 5.89 × yA nas equações yA e yB, obtemos duas equações com dois desconhecidos

Resolvendo duas equações com duas incógnitas, obtemos

x A = 7.37   m

y A = 0.823   m

Agora podemos resolver a tensão T0 com a equação T0 = 200 - 5,89 × yA. Temos todos os parâmetros para resolver esta equação.

T 0 = 200 - 5.89 × y A

T 0 = 200 - 5.89 × 0.823

T 0 = 195.2   N

s B - s A = T 0 μ sinh ⁡ μ x B T 0 - sinh ⁡ μ x A T 0                     x B = x A + 12 = 19.37

= 195.2 5.89 sinh ⁡ 5.89 × 19.37 195.2 - sinh ⁡ 5.89 × 7.37 195.2

= 13.06   m

Agora vamos determinar o ângulo no ponto A.

θ A = tan - 1 sinh ⁡ μ x A T 0

= tan - 1 sinh ⁡ 5.89 × 7.37 195.2

= 12.64 °

Passo 3

Usando a frase para resolver a tensão, obteremos o resultado para o ponto e B.

T B = T 0 + μ y B = 195.2 + 5.89 × 5.823 = 229   N

Resposta

θ = 12.64 °

T B = 229   N

s = 13.06   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga I suporta a força de 1000 lb e o par de 2000 lb-ft aplicado ao suporte de 2 pés soldado na extremidade da viga. Calcule o cisalhamento V e o momento M na seção intermediária entre A e B.
O cabo de massa desprezível é suspenso nos dois pontos fixos mostrados, e a tensão no suporte inferior é suficiente para manter a inclinação zero do cabo naquele ponto. O cabo suporta uma carga unitár
Uma luminária está suspensa no teto de um pórtico externo. Quatro correntes, duas das quais são mostradas, evitam o movimento excessivo do aparelho durante condições de vento. Se as correntes pesarem
O cabo de luz tem inclinação zero em seu ponto inferior de fixação e suporta a carga unitária que varia linearmente com x de w0 a w1 conforme mostrado. Derive a expressão para a tensão no cabo na orig
Ao lançar a âncora em 100 pés de água, um pequeno barco a motor inverte sua hélice, o que dá um empuxo reverso P = 800 lb. Um total de 400 pés de corrente da âncora à proa foi liberado. A corrente pes