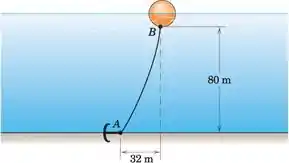
Uma bóia esférica usada para marcar o curso para uma corrida de veleiro é mostrada na figura. Existe uma corrente de água da esquerda para a direita que causa um arrasto horizontal na bóia; o efeito da corrente no cabo pode ser desprezado. O comprimento do cabo entre os pontos A e B é de 87 m, e a massa efetiva do cabo é de 2 kg / m quando a flutuabilidade do cabo é considerada. Determine as tensões em A e B.
Passo 1
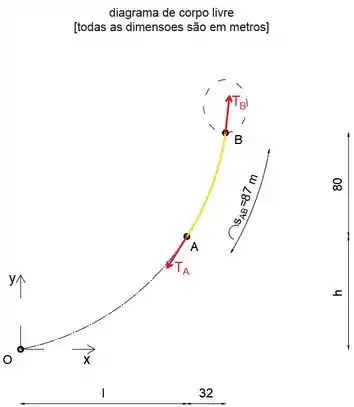
Primeiro, desenharemos o diagrama de corpo livre do cabo. Imagine que o cabo não termina em A, em vez disso, continua até chegar ao ponto mais baixo, esse ponto será marcado como o início do sistema de coordenadas.
Olhando para o esboço, podemos ver que as coordenadas dos pontos A e B são:
E o peso por unidade de comprimento é igual à massa por unidade de comprimento vezes a gravidade:
Passo 2
A seguir, uma vez que o cabo suporta apenas seu peso, o cabo tem uma forma conhecida como catenária, então usaremos a expressão (5/19)
Substitua por seu valor e coloque as coordenadas dos pontos A e B na equação.
Ponto A:
Ponto B:
Passo 3
Observe que, subtraindo a equação (A.1) e (B.1), eliminaremos o h desconhecido
Uma vez que existem duas incógnitas figurando na equação (1), precisaremos escrever outra equação onde essas duas (l e T0) são as únicas incógnitas.
Sabemos que o comprimento do cabo do ponto A ao B é:
Podemos escrever este comprimento como a diferença entre o comprimento do ponto O ao B e do ponto O ao A
Passo 4
Usando a expressão (5/20), podemos escrever sA e sB como:
Substitua sA e sB pelas expressões (A.2) e (B.2) na equação (2)
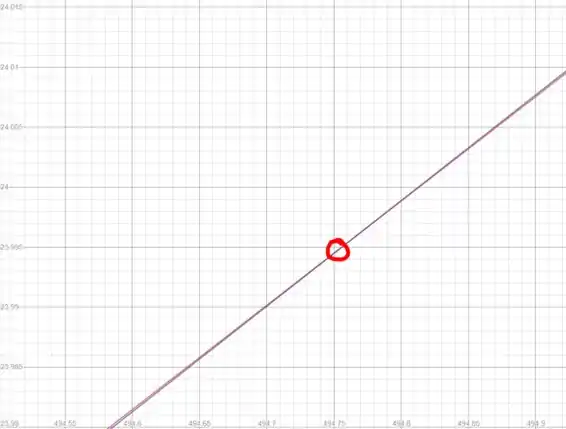
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos as equações (1) e (2.1) e leremos os valores de T0 e l que satisfazem ambas as equações.
Observe que você precisará ampliar o diagrama para poder ler os resultados.
Passo 5
Finalmente, usando a expressão (5/21) podemos determinar a tensão nos pontos A e B
Substitua T0 e por seus valores e coloque as coordenadas necessárias nas expressões acima.
Finalmente, substitua l por seu valor.
Calculando as expressões acima, obtemos que a tensão no cabo nos pontos A e B é: