Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 47
Determine a carga P necessária para provocar a falha por flambagem ou por escoamento da coluna W200 x 22 de aço A-36 engastada na base e livre no topo.
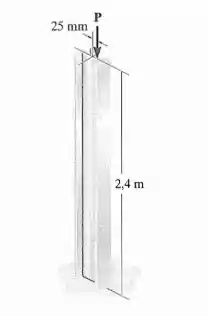
Passo 1
Falaaa!
Ele quer saber a carga máxima para que não haja flambagem e nem escoamento nessa coluna.
Como há excentricidade (a carga não está no centro da seção), a gente precisa testar a flambagem nas duas direções. Imagina que é a direção onde temos a distância entre o centro da seção e .
Vamos reunir nossos dados. A excentricidade é distante do eixo . Para o aço-36 nós temos:
E esse elemento que ele deu tem o momento de inércia e outras propriedades da seção em uma tabelinha nas últimas páginas do livro, no apêndice B. De lá, a gente tira que
É importante pegar a área da seção e altura da viga lá também, tá? Vamos usar mais a frente.
Temos que o comprimento da viga é . E como ela está engastada numa extremidade e livre na outra, .
Temos uma carga excêntrica em relação ao eixo . Mas ela é simples em relação a (já que ela está sobre o eixo ). Em cada situação usamos uma fórmula diferente, por isso, precisamos separar esse exercício em dois casos.
Passo 2
Primeiramente, vamos tratar da flambagem no eixo. A fórmula da carga crítica sem excentricidade para esse eixo é:
Substituindo os dados que a gente tem:
Passo 3
Conferindo se não há escoamento, precisamos calcular a tensão normal que essa força causa na nossa seção:
Dica: quando a gente divide (newtons) por , o resultado sai em . Aí vamos ter:
Como ela é menor que , essa carga não causa escoamento. E nossa força encontrada é válida.
Passo 4
No eixo , temos a excentricidade . Por isso devemos calcular alguns parâmetros para usar na fórmulinha:
Esse é a maior distância do eixo até a borda da seção, ou seja, a metade da altura da seção. E lembrando que
A fórmulinha que a gente tem para esse caso com , é a fórmula da tensão
Como a gente quer o que não causa escoamento, vamos usar a tensão de escoamento nessa fórmulinha para achar
Passo 5
Substituindo nossos dados:
Percebe que essa equação é super feia hehe. Não vai ser muito prático a gente resolver isso na não. Então vamos usar software, tipo um CAS ou alguma calculadora que resolve equações, tudo bem?
Conferindo se não há escoamento, precisamos calcular a tensão normal que essa força causa na nossa seção:
Dica: quando a gente divide (newtons) por , o resultado sai em . Aí vamos ter:
Como ela é menor que , essa carga não causa escoamento. E nossa força encontrada é válida.
Passo 6
Achamos dois valores para . Mas a gente precisa escolher o menor entre eles, porque a gente não quer que ocorra flambagem.
Se a gente escolhe o maior, quer dizer que já houve flambagem na outra direção.
Então nossa resposta final é