Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 67
O sistema mostrado na figura está em equilíbrio quando 0. Sabendo que inicialmente e que o bloco C está em movimento suave e muito lento quando o sistema está naquela posição, determine a velocidade do bloco quando ele passar pela posição de equilíbrio . Despreze o peso da barra.
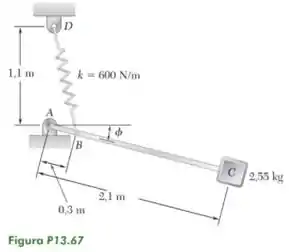
Fonte: Beer – Dinâmica – 9ª ed
Passo 1
Fala aí, tudo bem?
Vamos para mais um exercício do nosso lindo capítulo 13!
Bem, vamos analisar o problema de utilizando nossa amiga conservação de energia. Mas antes, devemos encontrar alguns valores que o problema não nos trouxe.
Façamos nossas considerações:
- Pelo enunciado, podemos desconsiderar a velocidade do sistema quando , assim a energia cinética nesse momento será nula;
- O problema quer a velocidade quando , nosso método de resolução será: Encontrar a energia mecânica nos dois momentos () e utilizar a conservação da energia, de forma que nossa única incógnita seja a velocidade em .
- Como iremos analisar os dois instantes, façamos nosso referencial (h = 0) o ponto onde , assim, nesse instante, a energia potencial gravitacional será nula.
Passo 2
Bem, analisemos primeiro quando :
Pode-se perceber que nesse instante teremos energia cinética, potencial gravitacional e potencial elástica.
Porém não temos argumentos suficientes para encontrar a energia potencial elástica. Para isso, devemos fazer o bom e velho diagrama do corpo livre, como no esboço abaixo:
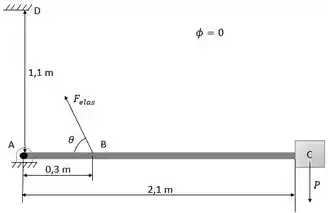
O ângulo formado entre a mola e a barra AC pode ser encontrado por um simples Pitágoras:
O comprimento pode ser encontrado por um simples Pitágoras:
Passo 3
Agora, fazendo o somatório do momento em A, temos:
Substituindo os valores:
Como sabemos que :
E (comprimento não alongado)
Vamos, então, encontrar a energia mecânica nesse instante:
Assim:
Passo 4
Analisando agora quando :
O nesse instante pode ser encontrado:
Assim, a energia mecânica nesse instante se dá por:
Assim:
Passo 5
Por fim, a conservação da energia nos diz que , então:
Fazendo os cálculos, encontramos que:
Resposta
Portanto: