Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 71
Um bloco de 300 g é liberado do repouso em A e desliza sem atrito ao longo da superfície mostrada na figura. Determine a força exercida sobre o bloco pela superfície (a) justamente antes de o bloco alcançar C e (b) imediatamente após ele passar por C.
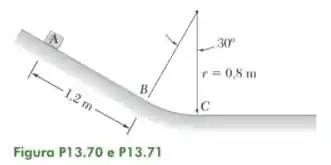
Fonte: Beer – Dinâmica – 9ª ed
Passo 1
Fala aí, tudo bem?
Tudo tranquilo até aqui? Esperamos que sim haha!
Bem, vamos analisar o problema de utilizando nossa amiga conservação de energia.
Façamos nossas considerações:
- Pelo enunciado, podemos desconsiderar a velocidade do sistema em A, assim a energia cinética nesse momento será nula;
- O problema quer a força exercida sobre o bloco, ele está se referindo à Força Normal;
- Antes de encontrar a Força Normal, devemos utilizar a equação da conservação da energia para encontrar a velocidade em C;
- Considerando o ponto C como nosso referencial, a energia potencial gravitacional nesse instante também será nula, facilitando nossos cálculos.
O esboço abaixo nos mostra os dois instantes:
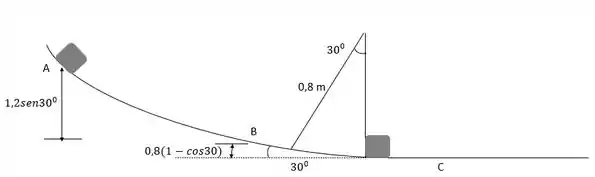
Passo 2
Letra a) Então, aplicando a conservação da energia, teremos somente:
Assim, antes do bloco alcançar C, a resultante das forças é a Força Centrípeta, dada por . Então:
Passo 3
Letra b) Imediatamente após o bloco passar pelo ponto C, ele entra retorna ao movimento retilíneo, ou seja, a resultante das forças volta a ser zero:
Resposta
Portanto:
Letra a)
Letra b)