Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 57
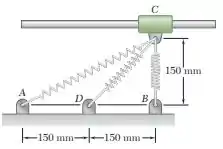
Um colar de 1,2 kg pode deslizar sem atrito ao longo da haste horizontal. Ele está preso a três molas, cada uma de constante e de comprimento indeformado. Sabendo que o colar é liberado do repouso na posição mostrada, determine a máxima velocidade que ele irá alcançar no movimento subsequente.
Passo 1
Vamos lá! Para determinarmos a máxima velocidade do bloco iremos utilizar o princípio de conservação de energia, que nos diz que:
De início sabemos que o bloco partirá do repouso. Portanto, .
Como queremos que a velocidade seja máxima, será necessário que a energia potencial, a qual tem apenas componente elástica nesta questão (não há variação de altura), seja mínima no ponto 2.
De fato, o ideal é que ela fosse nula. Mas, como isto não é possível nesta questão, nesta questão temos que minimizar a energia potencial elástica. Isto será conseguido quando estiver acima do ponto , com a mola sem estar deformada!
Agora, vamos aos cálculos da nossa questão.
Passo 2
Vamos começar calculando a energia potencial elástica no momento inicial, em que a mola não está deformada.
Calculando a deformação das outras duas molas, temos:
Portanto, a energia potencial inicial será:
Passo 3
Agora vamos calcular a energia potencial no ponto final, o qual está localizado acima do ponto . Neste caso, apenas as molas e estarão deformadas. Então, calculando a deformação das outras duas molas, temos:
Portanto, a energia potencial inicial será:
Passo 4
Para finalizarmos, vamos utilizar o princípio da conservação e energia para calcular a velocidade máxima. Portanto,
E assim finalizamos a nossa questão.