Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 56
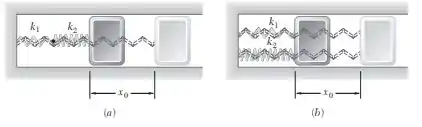
Um bloco de massa é fixado a duas molas como mostra a figura. Sabendo que em cada caso o bloco é puxado por uma distância de sua posição de equilíbrio e liberado, determine a máxima velocidade do bloco em seu movimento subsequente.
Passo 1
Vamos lá! Para determinarmos a máxima velocidade do bloco iremos utilizar o princípio de conservação de energia, que nos diz que:
De início sabemos que o bloco partirá do repouso. Portanto, .
Como queremos que a velocidade seja máxima, será necessário que a energia potencial, a qual tem apenas componente elástica nesta questão (não há variação de altura), seja nula no ponto 2. Logo, .
Portanto, chegamos a seguinte relação:
Passo 2
No final do Passo 1 encontramos a relação que devemos utilizar para calcular a velocidade máxima para cada caso.
Entretanto, faltou descrevermos quem é a constante de mola equivalente de cada sistema. Para isto, vamos utilizar as relações desenvolvidas na questão 55 para a mola equivalente. Para a letra a), em que as molas estão em séries, obtivemos:
Já para a letra b), como as molas estão em paralelo, temos:
Passo 3
Para finalizarmos a questão, basta substituirmos as relações descritas no Passo 2 na equação da velocidade do Passo 1. Portanto, para a letra a) temos:
Já para a letra b),
E assim finalizamos a questão!