Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 97

Uma esfera homogênea S, um cilindro uniforme C e um tubo fino P estão em contato quando são liberados a partir do repouso no declive mostrado na figura. Sabendo que todos os três objetos rolam sem deslizar, determine, após 4 s de movimento, a distância livre entre (a) o tubo e o cilindro, (b) o cilindro e a esfera.

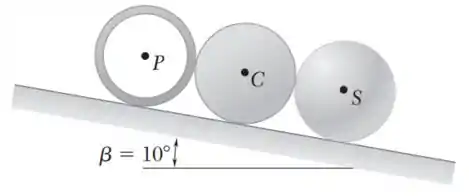
Passo 1

Caso geral:

I - = m k - 2 α - = r α

Σ M C e f f : ( w s e n ⁡ β ) r = I - α + m a - r m g s e n ⁡ β r = m k - 2 α + m r 2 α α = r θ s e n ⁡ β r 2 + k - 2

a - = r α = r r g s e n ⁡ β r 2 + k - 2 a - = r 2 r 2 + k - 2 g s e n ⁡ β

Para o cano:

k - = r                                                             a - P = r 2 r 2 + r 2 g s e n ⁡ β = 1 2 g s e n ⁡ β

Para o cilindro

k ² - = 1 2                                                             a - C = r 2 r 2 + r 2 2 g s e n ⁡ β = 2 3 g s e n ⁡ β

Para esféra

k ² - = 2 5                                                             a - E = r 2 r 2 + 2 5 r 2 g s e n ⁡ β = 5 7 g s e n ⁡ β

Passo 2

(a)Entre o cano e o cilindro

a C I P = a C - a P = 2 3 - 1 2 g s e n ⁡ β = 1 6 g s e n ⁡ β x C / P = 1 2 a C / P t 2 = 1 2 1 6 g s e n ⁡ β t 2

Unidade SI

x C / P = 1 2 1 6 9.81 m / s ² s e n 10 ° 4 s 2 = 2.27 m

Unidade US

Passo 3

(b)Entre a esfera e o cilindro

a E / C = a E - a C = 5 7 - 2 3 g s e n ⁡ β = 1 21 g s e n ⁡ β x E / C = 1 2 a E / C t 2 = 1 2 1 21 g s e n ⁡ β t 2

Unidade SI

x E / C = 1 2 1 21 9.81 m / s ² s e n 10 ° 4 s 2 = 0.649   m

Unidade US

Resposta

a = x C / P = 1 2 1 6 9.81 m / s ² s e n 10 ° 4 s 2 = 2.27 m

b = x E / C = 1 2 1 21 9.81 m / s ² s e n 10 ° 4 s 2 = 0.649   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O braço ABD está conectado por pinos ao colar em B e à manivela DE. Sabendo que a velocidade angular da manivela DE é de 1,2r a d/ s no sentido anti-horário, determine (a) a velocidade angular do braç
Dois rasgos foram abertos na placa F G e a placa foi posicionada de tal forma que os rasgos são ajustados a dois pinos fixos A e B . Sabendo que no instante mostrado na figura a velocidade angular da
Duas barras idênticas ABF e DBE estão conectadas por um pino em B. Sabendo que, no instante mostrado na figura, a velocidade no ponto D é de 250m m / s para cima, determine a velocidade (a) do ponto E
A barra AB é fixada ao colar em A e é equipada com uma pequena roda em B. Sabendo que quando θ = 60 ° a velocidade do colar é 250m m / s para cima, determine (a) a velocidade angular da barra AB, (b)
Dois colares C e D movem ao longo da barra vertical mostrada na figura. Sabendo que a velocidade do colar C é 660m m / s para baixo, determine (a) a velocidade do colar D , (b) a velocidade angular na